题目内容
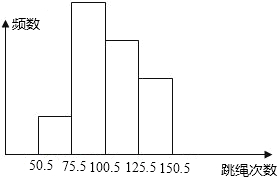 如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有
如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有
- A.6人
- B.8人
- C.16人
- D.20人
D
分析:从图得出一分钟跳绳次数在100次以上的即第三、四组所占比例,然后用:100次以上的学生数=总人数×比例,计算即可.
解答:从左起第一、二、三、四个小长方形的高的比为1:4:3:2,即各组频率之比为1:4:3:2;一分钟跳绳次数在100次以上的即第三、四组,所占比例为\frac{3+2}{1+4+3+2},即\frac{1}{2}.故有40×\frac{1}{2}=20人.
故选D.
点评:本题考查分析频数分布直方图和频率的求法.解本题要懂得频率分布直分图的意义,了解频率分布直分图是一种以频数为纵向指标的条形统计图.
分析:从图得出一分钟跳绳次数在100次以上的即第三、四组所占比例,然后用:100次以上的学生数=总人数×比例,计算即可.
解答:从左起第一、二、三、四个小长方形的高的比为1:4:3:2,即各组频率之比为1:4:3:2;一分钟跳绳次数在100次以上的即第三、四组,所占比例为\frac{3+2}{1+4+3+2},即\frac{1}{2}.故有40×\frac{1}{2}=20人.
故选D.
点评:本题考查分析频数分布直方图和频率的求法.解本题要懂得频率分布直分图的意义,了解频率分布直分图是一种以频数为纵向指标的条形统计图.

练习册系列答案
相关题目
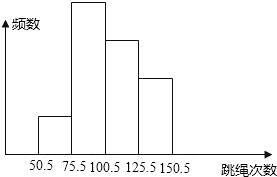 如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )
如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )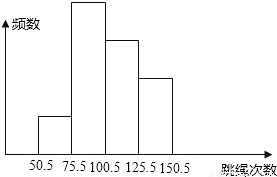 如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )
如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )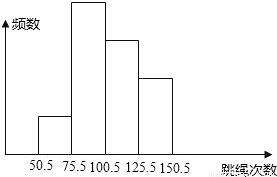 如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )
如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )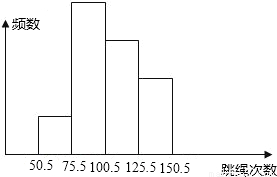 (2006•沈阳)如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )
(2006•沈阳)如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )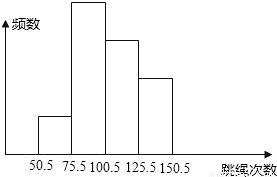 (2006•沈阳)如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )
(2006•沈阳)如图是某班40名学生一分钟跳绳测试成绩(次数为整数)的频数分布直方图,从左起第一、二、三、四个小长方形的高的比为1:4:3:2,那么该班一分钟跳绳次数在100次以上的学生有( )