题目内容
如图1,扇形AOB中,OA=10,∠AOB=36°.若固定B点,将此扇形依顺时针方向旋转,得一新扇形A′O′B,其中A点在O′B上,如图2所示,则O点旋转至O′点所经过的轨迹长度为( )
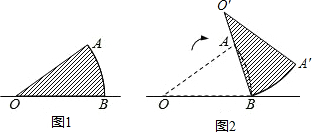

| A、π | B、2π | C、3π | D、4π |
分析:根据弧长公式,此题主要是得到∠OBO′的度数.根据等腰三角形的性质即可求解.
解答:解:根据题意,知OA=OB.
又∵∠AOB=36°,
∴∠OBA=72°.
∴点旋转至O′点所经过的轨迹长度=
=4π.
故选D.
又∵∠AOB=36°,
∴∠OBA=72°.
∴点旋转至O′点所经过的轨迹长度=
| 72×π×10 |
| 180 |
故选D.
点评:此题综合运用了等腰三角形的性质和弧长公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


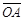 =10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在
=10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在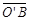 上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
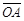 =10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在
=10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在 上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
 =10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在
=10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在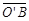 上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?