题目内容
如图,在一幅矩形地毯ABCD的四周镶有宽度都是1米的花边.设矩形地毯AB边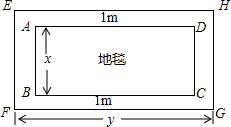 长为x米.镶有花边后,整个地毯EFGH中FG边长为y米.
长为x米.镶有花边后,整个地毯EFGH中FG边长为y米.
(1)若原地毯ABCD的周长为l8米,求y与x的函数关系式不要求写出自变量的取值范围);
(2)在(1)的条件下,当整个地毯EFGH的面积是40平方米,且AB<BC时,AB的长为多少米?
解:(1)∵y=BC+2=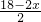 +2
+2
∴y=-x+11
(2)∵矩形EFGH的面积=EF×GH=(x+2)(-x+11)=40
∴-x2+9x+22=40
解得:x=3或x=6
当x=3时,即AB=3,则BC=6;
当x=6时,即AB=6,则BC=3
∵AB<BC
∴x=6(舍去)
答:AB的长为3米.
分析:(1)利用矩形的周长与边长之间的关系列出函数关系式即可;
(2)根据矩形EFGH的面积计算方法可以列出有关x的一元二次方程求解即可.
点评:本题主要考查了一元二次方程的应用,在解题时要能根据矩形的面积有关的信息列出方程是本题的关键.
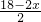 +2
+2∴y=-x+11
(2)∵矩形EFGH的面积=EF×GH=(x+2)(-x+11)=40
∴-x2+9x+22=40
解得:x=3或x=6
当x=3时,即AB=3,则BC=6;
当x=6时,即AB=6,则BC=3
∵AB<BC
∴x=6(舍去)
答:AB的长为3米.
分析:(1)利用矩形的周长与边长之间的关系列出函数关系式即可;
(2)根据矩形EFGH的面积计算方法可以列出有关x的一元二次方程求解即可.
点评:本题主要考查了一元二次方程的应用,在解题时要能根据矩形的面积有关的信息列出方程是本题的关键.

练习册系列答案
相关题目
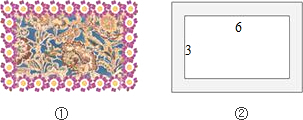 如图①,在一幅矩形地毯的四周镶有宽度相同的边.如图②,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米.求花边的宽.
如图①,在一幅矩形地毯的四周镶有宽度相同的边.如图②,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米.求花边的宽.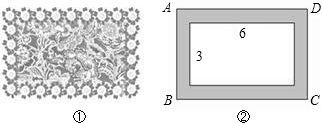
 长为x米.镶有花边后,整个地毯EFGH中FG边长为y米.
长为x米.镶有花边后,整个地毯EFGH中FG边长为y米. 如图①,在一幅矩形地毯的四周镶有宽度相同的边.如图②,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米.求花边的宽.
如图①,在一幅矩形地毯的四周镶有宽度相同的边.如图②,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米.求花边的宽.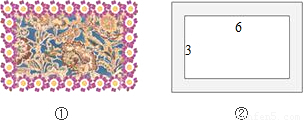 如图①,在一幅矩形地毯的四周镶有宽度相同的边.如图②,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米.求花边的宽.
如图①,在一幅矩形地毯的四周镶有宽度相同的边.如图②,地毯中央的矩形图案长6米、宽3米,整个地毯的面积是40平方米.求花边的宽.