题目内容
(2006•江西)一条抛物线y= x2+mx+n经过点(0,
x2+mx+n经过点(0, )与(4,
)与(4, ).
).(1)求这条抛物线的解析式,并写出它的顶点坐标;
(2)现有一半径为1,圆心P在抛物线上运动的动圆,当⊙P与坐标轴相切时,求圆心P的坐标.
【答案】分析:(1)将已知点的坐标代入抛物线中即可得出二次函数的解析式.进而可求出抛物线的顶点坐标;
(2)本题要分两种情况进行讨论:
①当圆与y轴相切时,那么圆心的横坐标的绝对值为1,可将其横坐标(分正负两个)代入抛物线的解析式中,即可求出P点的坐标;
②当圆与x轴相切时,那么圆心的纵坐标的绝对值为1,然后仿照①的方法即可求出P点的坐标.
解答:解:(1)由抛物线过(0, ),(4,
),(4, )两点,
)两点,
得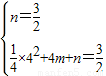 ,
,
解得 .
.
∴抛物线的解析式是:y= x2-x+
x2-x+ ,(3分)
,(3分)
由y= x2-x+
x2-x+ =
= (x-2)2+
(x-2)2+ ,得抛物线的顶点(2,
,得抛物线的顶点(2, );
);
(2)设点P的坐标为(x,y)
①当圆P与y轴相切时,有|x|=1,
∴x=±1
由x=1,得y= ×1-1+
×1-1+ =
=
由x=-1,得y= ×(-1)2-(-1)+
×(-1)2-(-1)+ =
=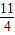
此时,点P的坐标为P1(1, ),P2(-1,
),P2(-1,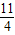 );
);
②当圆P与x轴相切时,有|y|=1
∵抛物线的开口向上,顶点在x轴的上方,y>0,∴y=1
由y=1,得 x2-x+
x2-x+ =1
=1
解得x=2±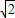
此时,点P的坐标为P1(2-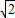 ,1),P4(2+
,1),P4(2+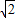 ,1)
,1)
综上所述,圆心P的坐标为P1(1, ),P2(-1,
),P2(-1,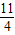 ),P3(
),P3(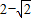 ,1),P4(
,1),P4(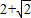 ,1).
,1).
点评:本题主要考查了二次函数解析式的确定以及切线的判定,要注意的是(2)题中要分与x轴相切和与y轴相切两种情况进行讨论,不要漏解.
(2)本题要分两种情况进行讨论:
①当圆与y轴相切时,那么圆心的横坐标的绝对值为1,可将其横坐标(分正负两个)代入抛物线的解析式中,即可求出P点的坐标;
②当圆与x轴相切时,那么圆心的纵坐标的绝对值为1,然后仿照①的方法即可求出P点的坐标.
解答:解:(1)由抛物线过(0,
 ),(4,
),(4, )两点,
)两点,得
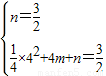 ,
,解得
 .
.∴抛物线的解析式是:y=
 x2-x+
x2-x+ ,(3分)
,(3分)由y=
 x2-x+
x2-x+ =
= (x-2)2+
(x-2)2+ ,得抛物线的顶点(2,
,得抛物线的顶点(2, );
);(2)设点P的坐标为(x,y)
①当圆P与y轴相切时,有|x|=1,
∴x=±1
由x=1,得y=
 ×1-1+
×1-1+ =
=
由x=-1,得y=
 ×(-1)2-(-1)+
×(-1)2-(-1)+ =
=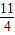
此时,点P的坐标为P1(1,
 ),P2(-1,
),P2(-1,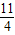 );
);②当圆P与x轴相切时,有|y|=1
∵抛物线的开口向上,顶点在x轴的上方,y>0,∴y=1
由y=1,得
 x2-x+
x2-x+ =1
=1解得x=2±
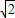
此时,点P的坐标为P1(2-
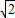 ,1),P4(2+
,1),P4(2+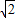 ,1)
,1)综上所述,圆心P的坐标为P1(1,
 ),P2(-1,
),P2(-1,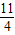 ),P3(
),P3(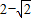 ,1),P4(
,1),P4(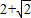 ,1).
,1).点评:本题主要考查了二次函数解析式的确定以及切线的判定,要注意的是(2)题中要分与x轴相切和与y轴相切两种情况进行讨论,不要漏解.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
(2006•江西)一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩一平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
友情提示:一组数据的标准差计算公式是S= ,其中
,其中 为n个数据x1,x2,…xnr的平均数.
为n个数据x1,x2,…xnr的平均数.
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 |  | |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩一平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
友情提示:一组数据的标准差计算公式是S=
 ,其中
,其中 为n个数据x1,x2,…xnr的平均数.
为n个数据x1,x2,…xnr的平均数. x2+mx+n经过点(0,
x2+mx+n经过点(0, )与(4,
)与(4, ).
).
 x2+mx+n经过点(0,
x2+mx+n经过点(0, )与(4,
)与(4, ).
).
 x2+mx+n经过点(0,
x2+mx+n经过点(0, )与(4,
)与(4, ).
).