题目内容
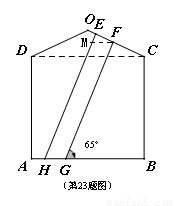
(本题满分10分)一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°。
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m)。
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
【答案】
(1)在四边形BCFG中,∠GFC=360°-90°-65°-(90°+25°)=90°
则GF⊥OC
(2)如图,作FM∥GH交EH与M, 则有平行四边形FGHM,
 ∴FM=GH=2.6m,∠EFM=25°
∴FM=GH=2.6m,∠EFM=25°
∵FG∥EH,GF⊥OC
∴EH⊥OC
在Rt△EFM中:
EF=FM·cos25°≈2.6×0.91=2.4m
【解析】略

练习册系列答案
相关题目
(本题满分10分)
一次科技知识竞赛,两个班学生的成绩如下:
(1)请分别求出两个班成绩的众数与中位数.
(2)若规定100分为一等奖,90分为二等奖,80分为三等奖,请分别求出两个班的获奖率.
(3)请分别求出两个班成绩的方差.
一次科技知识竞赛,两个班学生的成绩如下:
| 分数(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 甲班人数(人) | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙班人数(人) | 4 | 4 | 16 | 2 | 12 | 12 |
(2)若规定100分为一等奖,90分为二等奖,80分为三等奖,请分别求出两个班的获奖率.
(3)请分别求出两个班成绩的方差.
(本题满分10分)
一次科技知识竞赛,两个班学生的成绩如下:
|
分数(分) |
50 |
60 |
70 |
80 |
90 |
100 |
|
甲班人数(人) |
2 |
5 |
10 |
13 |
14 |
6 |
|
乙班人数(人) |
4 |
4 |
16 |
2 |
12 |
12 |
(1)请分别求出两个班成绩的众数与中位数.
(2)若规定100分为一等奖,90分为二等奖,80分为三等奖,请分别求出两个班的获奖率.
(3)请分别求出两个班成绩的方差.