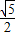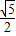题目内容
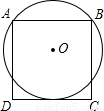
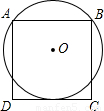
（2006•扬州）如图，已知⊙O过正方形ABCD的顶点A、B，且与CD边相切，若正方形的边长为2，则圆的半径为（ ）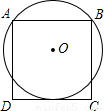
A．
B．
C．
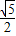
D．1
【答案】分析：过点O作OE⊥AB，连接OB，在Rt△OBE中，根据勾股定理可将半径OB的长求出．
解答：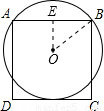
解：过点O作OE⊥AB，交AB于点E，连接OB，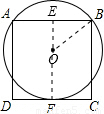
设⊙O的半径为R，∵正方形的边长为2，CD与⊙O相切，
∴OF=R，
∴OE=2-R，
在Rt△OBE中，
OE2+EB2=OB2，即（2-R）2+12=R2，解得R=
．
故选B．
点评：本题考查了圆的切线性质，及解直角三角形的知识．
解答：
解：过点O作OE⊥AB，交AB于点E，连接OB，设⊙O的半径为R，∵正方形的边长为2，CD与⊙O相切，
∴OF=R，
∴OE=2-R，
在Rt△OBE中，
OE2+EB2=OB2，即（2-R）2+12=R2，解得R=
．故选B．
点评：本题考查了圆的切线性质，及解直角三角形的知识．
练习册系列答案
相关题目
