题目内容
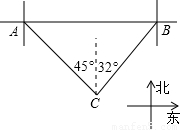
如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?(精确到1米,参考数据:sin32°=0.5299,cos32°=0.8480)
【答案】分析:本题可通过构建直角三角形来解答,过点C作AB的垂线交AB于D,CD是直角三角形ACD和CBD的公共直角边,要先求出CD的值然后再求AD,BD的值,进而得出AB的长.
解答: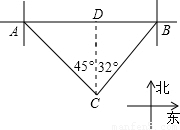 解:过点C作AB的垂线交AB于D,
解:过点C作AB的垂线交AB于D,
∵B点在A点的正东方向上,
∴∠ACD=45°,∠DCB=32°,
在Rt△BCD中,BC=100,
∴DB=BCsin32°≈1000.5299=52.99(米),
CD=BCcos32°≈1000.8480=84.80(米),
在Rt△ACD中,AD=CD,
∴AB=AD+DB≈84.80+52.99=137.79(米)≈138(米).
点评:本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,如果两个直角三角形有公共的直角边,先求出公共边一般是解题的常用方法.
解答:
 解:过点C作AB的垂线交AB于D,
解:过点C作AB的垂线交AB于D,∵B点在A点的正东方向上,
∴∠ACD=45°,∠DCB=32°,
在Rt△BCD中,BC=100,
∴DB=BCsin32°≈1000.5299=52.99(米),
CD=BCcos32°≈1000.8480=84.80(米),
在Rt△ACD中,AD=CD,
∴AB=AD+DB≈84.80+52.99=137.79(米)≈138(米).
点评:本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,如果两个直角三角形有公共的直角边,先求出公共边一般是解题的常用方法.

练习册系列答案
相关题目
 18、如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?
18、如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?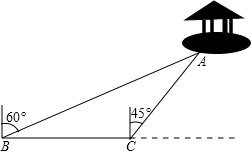 已知:如图,某风景区的湖心岛有一凉亭A,小明想测量A到湖边的距离,他从湖边的B处测得A在北偏东60°的方向上,在C处测得A在北偏东45°的方向上,且量得B、C两点之间的距离为10米.根据上述测量结果,请你帮小明计算凉亭A到湖边的距离.
已知:如图,某风景区的湖心岛有一凉亭A,小明想测量A到湖边的距离,他从湖边的B处测得A在北偏东60°的方向上,在C处测得A在北偏东45°的方向上,且量得B、C两点之间的距离为10米.根据上述测量结果,请你帮小明计算凉亭A到湖边的距离.