题目内容
 已知等边△ABC内接于⊙O,点P是劣弧
已知等边△ABC内接于⊙O,点P是劣弧 | BC |
(1)若AP过圆心O,如图1,且圆O的直径为10cm,求CD的长;
(2)若AP不过圆心O,如图2,PC=3cm,求PD的长.
分析:(1)根据等边三角形的性质得到AC=BC,∠BAC=60°,又AP过圆心O可得到AP平分∠CAB,AP为直径,根据直径所对的圆周角为直角得到∠ACP=90°,再利用含30°的直角三角形三边的关系得到CP=
AP=
×10=5(cm),利用圆周角定理可得到∠CAP=∠CBP,易证得△CAP≌△CBD,则CP=CD,根据圆内接四边形的性质得到∠CPD=∠CAB=60°,则△PCD为等边三角形,于是CD=PC=5cm;
(2)与(1)的证明方法一样可得到△PCD为等边三角形,则CD=PC=3cm.
| 1 |
| 2 |
| 1 |
| 2 |
(2)与(1)的证明方法一样可得到△PCD为等边三角形,则CD=PC=3cm.
解答:解:(1)∵△ABC为等腰三角形,
∴AC=BC,∠BAC=60°,
∵AP过圆心O,
∴AP平分∠CAB,AP为直径,
∴∠CAP=30°,∠ACP=90°,
∴CP=
AP=
×10=5(cm),
在△CAP和△CBD中
∵
,
∴△CAP≌△CBD,
∴CP=CD,
∵∠CPD=∠CAB=60°,
∴△PCD为等边三角形,
∴CD=PC=5cm;
(2)与(1)一样可证明得到△CAP≌△CBD,
则CP=CD,
∵∠CPD=∠CAB=60°,
∴△PCD为等边三角形,
∴CD=PC=3cm.
∴AC=BC,∠BAC=60°,
∵AP过圆心O,
∴AP平分∠CAB,AP为直径,
∴∠CAP=30°,∠ACP=90°,
∴CP=
| 1 |
| 2 |
| 1 |
| 2 |
在△CAP和△CBD中
∵
|
∴△CAP≌△CBD,
∴CP=CD,
∵∠CPD=∠CAB=60°,
∴△PCD为等边三角形,
∴CD=PC=5cm;
(2)与(1)一样可证明得到△CAP≌△CBD,
则CP=CD,
∵∠CPD=∠CAB=60°,
∴△PCD为等边三角形,
∴CD=PC=3cm.
点评:本题考查了圆的综合题:在同圆或等圆中,同弧所对的圆周角相等;直径所对的圆周角为直角;圆的内接四边形的性质在几何证明中也常用到.

练习册系列答案
相关题目
 已知等边△ABC内接于⊙O,点D是⊙O上任意一点,则sin∠ADB的值为( )
已知等边△ABC内接于⊙O,点D是⊙O上任意一点,则sin∠ADB的值为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
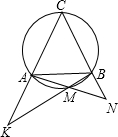 如图,已知等边△ABC内接于圆,在劣弧AB上取异于A、B的点M,设直线AC与BM相交于K,直线CB与AM相交于点N,
如图,已知等边△ABC内接于圆,在劣弧AB上取异于A、B的点M,设直线AC与BM相交于K,直线CB与AM相交于点N, 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.



