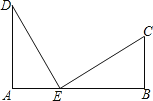
题目内容
【题目】如图，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，求∠AEC的度数．
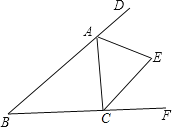
【答案】66.5°
【解析】试题分析：根据三角形内角和定理、角平分线的定义以及三角形外角定理求得
∠DAC+
∠ACF=
（∠B+∠B+∠1+∠2）=
；最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数．
试题解析：
∵三角形的外角∠DAC和∠ACF的平分线交于点E，
∴∠EAC=
∠DAC，∠ECA=
∠ACF；
又∵∠B=47°（已知），∠B+∠1+∠2=180°（三角形内角和定理），
∴
∠DAC+
∠ACF=
（∠B+∠2）+
（∠B+∠1）=
（∠B+∠B+∠1+∠2）=
（外角定理），
∴∠AEC=180°﹣（
∠DAC+
∠ACF）=66.5°；
故答案是：66.5°．
练习册系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如下尚不完整的统计图表．
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 |
（1）在图1中，“7分”所在扇形的圆心角等于 °．
（2）请你将图2的统计图补充完整；
（3）经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好．
（4）如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？
