题目内容
观察下面两图形的形成过程，若AD=3，DB=4，则△ADE和△BDF面积的和为 ．
【答案】分析：由图形的旋转可知，图形顺时针旋转了90°，即∠EDF=∠ADA′=90°，可得∠ADB=90°，△ADE和△BDF面积的和即为△A′DB的面积．
解答：解：观察图形的旋转可知：旋转角∠EDF=∠ADA′=90°，AD=A′D=3，
∴∠A′DB=180°-∠ADA′=90°，
∴S△ADE+S△BDF=S△A′BD=
×A′D×BD=6．
故答案为：6．
点评：本题考查了旋转的性质，通过旋转将两个图形“移”到同一个图形中去，便于计算面积．
解答：解：观察图形的旋转可知：旋转角∠EDF=∠ADA′=90°，AD=A′D=3，
∴∠A′DB=180°-∠ADA′=90°，
∴S△ADE+S△BDF=S△A′BD=
×A′D×BD=6．故答案为：6．
点评：本题考查了旋转的性质，通过旋转将两个图形“移”到同一个图形中去，便于计算面积．
练习册系列答案
教材全解字词句篇系列答案
相关题目
观察下面两图形的形成过程，若AD=3，DB=4，则△ADE和△BDF面积的和为
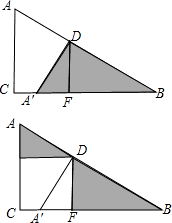观察下面两图形的形成过程，若AD=3，DB=4，则△ADE和△BDF面积的和为________．