题目内容
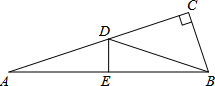 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.(1)若AD=15,cos∠BDC=
| 4 |
| 5 |
(2)设∠BDC=α,计算tan
| α |
| 2 |
考点:解直角三角形
专题:计算题
分析:(1)由线段垂直平分线的性质得DB=DA=15,再根据余弦的定义得到cos∠BDC=
=
,则DC=12,根据勾股定理可计算出BC=9,然后在Rt△ACB中,根据正切的定义求解;
(2)设AD=t,则DB=t,根据正、余弦的定义得到DC=t•cosα,BC=t•sinα,再根据正切的定义tanA=
=
,然后证明∠A=
即可.
| DC |
| DB |
| 4 |
| 5 |
(2)设AD=t,则DB=t,根据正、余弦的定义得到DC=t•cosα,BC=t•sinα,再根据正切的定义tanA=
| BC |
| AC |
| sinα |
| sinα+cosα |
| α |
| 2 |
解答:解:(1)∵DE垂直平分AB,
∴DB=DA=15,
在Rt△DCB中,cos∠BDC=
=
,
∴
=
,
∴DC=12,
∴BC=
=9,
在Rt△ACB中,AC= AD+CD=27,
AD+CD=27,
∴tanA=
=
=
;
(2)设AD=t,则DB=t,
在Rt△DCB中,
∵cos∠BDC=
,sin∠BDC=
,
∴DC=t•cosα,BC=t•sinα,
在Rt△ACB中,AC=AD+DC=t(sinα+cosα),
∴tanA=
=
=
,
∵AD=DB,
∴∠A=∠DBA,
∴∠BDC=∠A+∠DBA=2∠A,
∴∠A=
,
∴tan
=
.
∴DB=DA=15,
在Rt△DCB中,cos∠BDC=
| DC |
| DB |
| 4 |
| 5 |
∴
| DC |
| 15 |
| 4 |
| 5 |
∴DC=12,
∴BC=
| BD2-DC2 |
在Rt△ACB中,AC=
 AD+CD=27,
AD+CD=27,∴tanA=
| BC |
| AC |
| 9 |
| 27 |
| 1 |
| 3 |
(2)设AD=t,则DB=t,
在Rt△DCB中,
∵cos∠BDC=
| DC |
| DB |
| BC |
| BD |
∴DC=t•cosα,BC=t•sinα,
在Rt△ACB中,AC=AD+DC=t(sinα+cosα),
∴tanA=
| BC |
| AC |
| t•sinα |
| t(sinα+cosα) |
| sinα |
| sinα+cosα |
∵AD=DB,
∴∠A=∠DBA,
∴∠BDC=∠A+∠DBA=2∠A,
∴∠A=
| α |
| 2 |
∴tan
| α |
| 2 |
| sinα |
| sinα+cosα |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了线段垂直平分线的性质.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
2012年雁荡山风景区全年共接待国内外游客约为3 250 000人次,该数据用科学记数法表示为( )
| A、3.25×107 |
| B、3.25×106 |
| C、0.325×107 |
| D、325×104 |
若2x=3y,则
的值为( )
| x |
| y |
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知点A(2,-2)和点B(-4,n)在抛物线y=ax2(a≠0)上.
已知点A(2,-2)和点B(-4,n)在抛物线y=ax2(a≠0)上.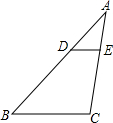 如图,△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD=2,DB=3,DE=1,则BC的长是
如图,△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD=2,DB=3,DE=1,则BC的长是