��Ŀ����
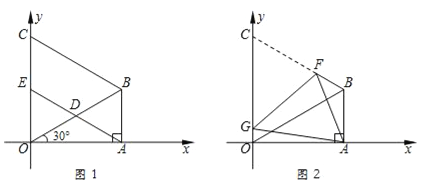
����Ŀ����ͼ1��ֱ��![]() ��x���ڵ�A����y���ڵ�C��0��4����������
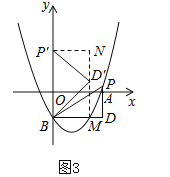
��x���ڵ�A����y���ڵ�C��0��4����������![]() ������A����y���ڵ�B��0����2������PΪ��������һ�����㣬����P��x��Ĵ���PD������B��BD��PD�ڵ�D������PB�����P�ĺ�����Ϊm��
������A����y���ڵ�B��0����2������PΪ��������һ�����㣬����P��x��Ĵ���PD������B��BD��PD�ڵ�D������PB�����P�ĺ�����Ϊm��
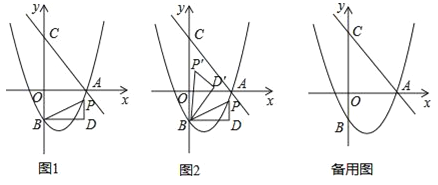
��1���������ߵĽ���ʽ��
��2������BDPΪ����ֱ��������ʱ�����߶�PD�ij���
��3����ͼ2������BDP�Ƶ�B��ʱ����ת���õ���BD��P�䣬����ת�ǡ�PBP��=��OAC������P�Ķ�Ӧ��P��������������ʱ����ֱ��д����P�����꣮
���𰸡���1��![]() ����2��PD=
����2��PD=![]() ��PD=
��PD=![]() ����3��P����
����3��P����![]() ��
��![]() ����P��
����P��![]() ��
��![]() ����P��
����P��![]() ��
��![]() ����
����
��������
�����������1����ȷ������A�����꣬���ô���ϵ������������߽���ʽ��
��2���ɡ�BDPΪ����ֱ�������Σ��жϳ�BD=PD������m�ķ��̼����m���Ӷ����PD��
��3���ֵ�P������x���y������������㼴�ɣ�
�����������1���ߵ�C��0��4����ֱ��![]() �ϣ���n=4����
�ϣ���n=4����![]() ����y=0����x=3����A��3��0������������
����y=0����x=3����A��3��0������������![]() ������A����y���ڵ�B��0����2������c=��2��6+3b��2=0����b=
������A����y���ڵ�B��0����2������c=��2��6+3b��2=0����b=![]() ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2����PΪ��������һ�����㣬���P�ĺ�����Ϊm����P��m��![]() ������BD=|m|��PD=
������BD=|m|��PD=![]() =
=![]() ���ߡ�BDPΪ����ֱ�������Σ���PD��BD����BD=PD����|m|=
���ߡ�BDPΪ����ֱ�������Σ���PD��BD����BD=PD����|m|=![]() ����m=0���ᣩ��m=
����m=0���ᣩ��m=![]() ��m=
��m=![]() ����PD=
����PD=![]() ��PD=
��PD=![]() ��
��
��3���ߡ�PBP'=��OAC��OA=3��OC=4����AC=5����sin��PBP'=![]() ��cos��PBP'=
��cos��PBP'=![]() ��������������ۣ�
��������������ۣ�
�ٵ���P'����x����ʱ������D'��D'N��x�ᣬ����ΪN����BD�ڵ�M����DBD'=��ND'P'=��PBP'����ͼ1��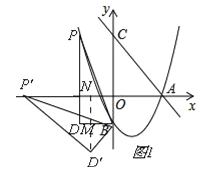
ND'��MD'=2����![]() ����m=
����m=![]() ���ᣩ����m=��
���ᣩ����m=��![]() ��
��
��ͼ2�� ND'+MD'=2����![]() ����m=
����m=![]() ����m=��
����m=��![]() ���ᣩ����P����
���ᣩ����P����![]() ��
��![]() ����P��
����P��![]() ��
��![]() ����
����
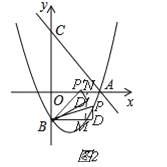
�ڵ���P'����y����ʱ����ͼ3������D����D��M��x�ᣬ��BD��M����P����P��N��y�ᣬ���DBD��=��ND��P��=��PBP�䣬��P��N=BM����![]() ����m=
����m=![]() ����P��
����P��![]() ��
��![]() ����
����
����������P����![]() ��
��![]() ����P��
����P��![]() ��
��![]() ����P��
����P��![]() ��
��![]() ����
����