题目内容
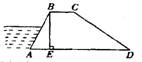
 如图,某河堤的横断面是梯形ABCD,BC∥AD,BE⊥AD于点E,AB=50米,BC=30米,∠A=60°,∠D=30°.求AD的长度.
如图,某河堤的横断面是梯形ABCD,BC∥AD,BE⊥AD于点E,AB=50米,BC=30米,∠A=60°,∠D=30°.求AD的长度.分析:作CF⊥AD交AD于点F,在Rt△ABE中,根据AB=50米,∠A=60°,求出BE、AE的长,然后再Rt△CFD中,根据∠D=30°,求出FD的长,又BC=EF,即可求出AD的长度.
解答:解:作CF⊥AD于点F,
∵BE⊥AD,AB=50米,∠A=60°,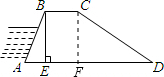
∴BE=ABsin60°=50×
=25
,
∴AE=
=25,
∵BC∥AD,CF⊥AD
∴CF=BE=25,EF=BC=30,
在Rt△CFD中,∠D=30°,
∴FD=
=
=75,
∴AD=AE+EF+FD=25+30+75=130(米).
∵BE⊥AD,AB=50米,∠A=60°,

∴BE=ABsin60°=50×
| ||
| 2 |
| 3 |
∴AE=
| AB2-BE2 |
∵BC∥AD,CF⊥AD
∴CF=BE=25,EF=BC=30,
在Rt△CFD中,∠D=30°,
∴FD=
| CF |
| tan30° |
25
| ||||
|
∴AD=AE+EF+FD=25+30+75=130(米).
点评:本题考查了解直角三角形的应用,难度一般,解答本题的关键是根据解直角三角形的知识求出BE,FD的长度.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
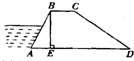 14、如图,某河堤的横断面是梯形ABCD,BC∥AD,已知背水坡CD的坡度i=1:2.4,CD长为13米,则河堤的高BE为
14、如图,某河堤的横断面是梯形ABCD,BC∥AD,已知背水坡CD的坡度i=1:2.4,CD长为13米,则河堤的高BE为 如图,某河堤的横断面是梯形,BC∥AD,迎水坡AB长13米,且坡度为1:2.4,则河堤高BE为
如图,某河堤的横断面是梯形,BC∥AD,迎水坡AB长13米,且坡度为1:2.4,则河堤高BE为