题目内容
(2008•北京)已知:关于x的一元二次方程mx2-(3m+2)x+2m+2=0(m>0).(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1<x2).若y是关于m的函数,且y=x2-2x1,求这个函数的解析式;
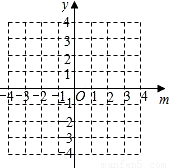
(3)在(2)的条件下,结合函数的图象回答:当自变量m的取值范围满足什么条件时,y≤2m.
【答案】分析:(1)本题的突破口在于利用△.化简得出(m+2)2>0得出△>0.
(2)由求根公式得出x的解,由y=x2-2x1求出关于m的解析式.
解答:(1)证明:∵mx2-(3m+2)x+2m+2=0是关于x的一元二次方程,
∴△=[-(3m+2)]2-4m(2m+2)=m2+4m+4=(m+2)2.
∵当m>0时,(m+2)2>0,即△>0.
∴方程有两个不相等的实数根.(2分)
(2)解:由求根公式,得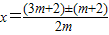 .
.
∴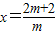 或x=1.(3分)
或x=1.(3分)
∵m>0,
∴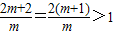 .
.
∵x1<x2,
∴x1=1,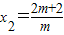 .(4分)
.(4分)
∴y=x2-2x1=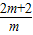 -2×1=
-2×1=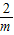 .
.
即y=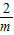 (m>0)为所求.(5分)
(m>0)为所求.(5分)
(3)解:在同一平面直角坐标系中分别画出y=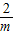 (m>0)与y=2m(m>0)的图象.(6分)
(m>0)与y=2m(m>0)的图象.(6分)
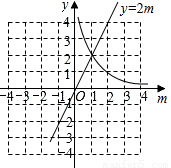
由图象可得,当m≥1时,y≤2m.(7分)
点评:本题是一道代数综合题,综合了一元二次方程、一次函数、用函数的观点看不等式等知识.
(2)由求根公式得出x的解,由y=x2-2x1求出关于m的解析式.
解答:(1)证明:∵mx2-(3m+2)x+2m+2=0是关于x的一元二次方程,
∴△=[-(3m+2)]2-4m(2m+2)=m2+4m+4=(m+2)2.
∵当m>0时,(m+2)2>0,即△>0.
∴方程有两个不相等的实数根.(2分)
(2)解:由求根公式,得
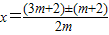 .
.∴
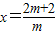 或x=1.(3分)
或x=1.(3分)∵m>0,
∴
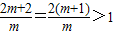 .
.∵x1<x2,
∴x1=1,
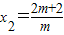 .(4分)
.(4分)∴y=x2-2x1=
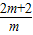 -2×1=
-2×1=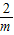 .
.即y=
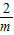 (m>0)为所求.(5分)
(m>0)为所求.(5分)(3)解:在同一平面直角坐标系中分别画出y=
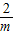 (m>0)与y=2m(m>0)的图象.(6分)
(m>0)与y=2m(m>0)的图象.(6分)
由图象可得,当m≥1时,y≤2m.(7分)
点评:本题是一道代数综合题,综合了一元二次方程、一次函数、用函数的观点看不等式等知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目