题目内容
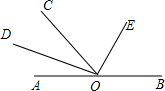
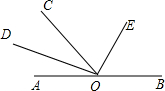
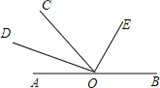
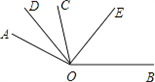
己知OD平分∠AOC,OE平分∠COB.(1)如图,若O是直线AB上的一点,求∠DOE的度数;
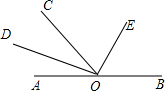
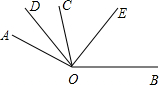
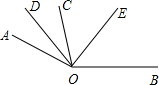
(2)如图,如果∠DOE=80°,那么∠AOB的度数是
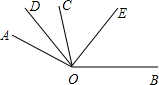
(3)(2)题中,设∠DOE=n° (0<n<90),求∠AOB的度数.
分析:(1)由于OD平分∠AOC,OE平分∠COB,所以∠DOE=
∠AOB=90°.
(2)由已知条件知,∠DOE=
∠AOB,所以∠AOB=2∠DOE.
(3)由(2)知,∠AOB=2∠DOE=2n°.
| 1 |
| 2 |
(2)由已知条件知,∠DOE=
| 1 |
| 2 |
(3)由(2)知,∠AOB=2∠DOE=2n°.
解答:解:(1)∵OD平分∠AOC,
∴∠AOD=∠COD=
∠AOC,
同理,∠COE=∠BOE=
∠COB,
∵∠AOC+∠COB=180°,
∴∠COD+∠BOE=
∠AOC+
∠COB=
(∠AOC+∠COB)=
×180°=90°.
即∠DOE=90°
(2)∵OD平分∠AOC,
∴∠AOD=∠COD=
∠AOC,
同理,∠COE=∠BOE=
∠COB,
∴∠COD+∠BOE=
∠AOC+
∠COB=
(∠AOC+∠COB),
即∠DOE=
∠AOB,
∵∠DOE=80°,
∴∠AOB=160°.
(3)由(2)知,∠AOB=2∠DOE=2n°.
∴∠AOD=∠COD=
| 1 |
| 2 |
同理,∠COE=∠BOE=
| 1 |
| 2 |
∵∠AOC+∠COB=180°,
∴∠COD+∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠DOE=90°
(2)∵OD平分∠AOC,
∴∠AOD=∠COD=
| 1 |
| 2 |
同理,∠COE=∠BOE=
| 1 |
| 2 |
∴∠COD+∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠DOE=
| 1 |
| 2 |
∵∠DOE=80°,
∴∠AOB=160°.
(3)由(2)知,∠AOB=2∠DOE=2n°.
点评:角的比较与运算,常常结合角平分线的知识来考查,充分利用隐含条件(平角,直角)是解题的关键.

练习册系列答案
相关题目