题目内容
【题目】如图,OABC中顶点A在x轴负半轴上,B、C在第二象限,对角线交于点D,若C、D两点在反比例函数![]() 的图象上,且OABC的面积等于12,则k的值是____.
的图象上,且OABC的面积等于12,则k的值是____.

【答案】﹣4
【解析】
过点D作DF⊥OA于点F,过点C作CE⊥OA于点E,由OABC的面积等于12,可得△AOC的面积为6,又因点D是线段AC的中点,CE∥DF,可得DF是△ACE的中位线,由三角形的中位线定理可得CE=2DF,AF=EF,根据反比例函数系数k的几何意义可得S△OCE=S△ODF= ![]() ,即可求得OF=2OE,S△ADF=
,即可求得OF=2OE,S△ADF= ![]() ,S△ACE=|k|,根据S△ACE+S△OCE=S△AOC=6可求得k值,根据反比例函数在第二象限对k的值进行取舍即可.
,S△ACE=|k|,根据S△ACE+S△OCE=S△AOC=6可求得k值,根据反比例函数在第二象限对k的值进行取舍即可.
解:如图所示:过点D作DF⊥OA于点F,过点C作CE⊥OA于点E,
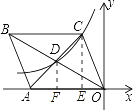
∵OABC的面积等于12,
∴△AOC的面积为6,
∵点D是线段AC的中点,CE∥DF,
∴DF是△ACE的中位线,
∴CE=2DF,AF=EF,
又∵S△OCE=S△ODF= ![]() ,
,
∴OF=2OE,S△ADF= ![]() ,S△ACE=|k|,
,S△ACE=|k|,
∴S△ACE+S△OCE=S△AOC=6,即 ![]() =6,
=6,
又∵k<0(反比例函数在第二象限),
∴k=﹣4.
故答案为:﹣4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目