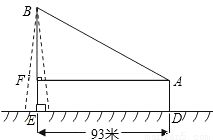
题目内容
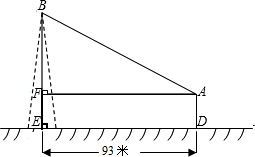
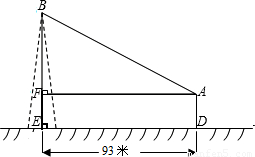
如图,在离铁塔93米的A处,用测角器测得塔顶的仰角为∠BAF,已知测角器高A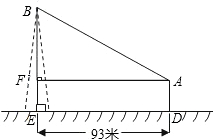 D=1.55米,请你解答以下两小题中的任意一个小题
D=1.55米,请你解答以下两小题中的任意一个小题
(1)若∠BAF=31°,求铁塔高BE(精确到0.01米).
(2)若∠BAF=30°,求铁塔高BE(精确到0.01米),提供参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
解:(1)在Rt△ABF中,
∵tan∠BAF=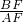
∴BF=AF•tan∠BAF=93×tan31°≈55.880(米)
∴BE=BF+FE=BF+AD≈55.880+1.55=57.430≈57.43(米)
答:铁塔高BE约长为57.43米.
(2)在Rt△ABF中,
∵tan∠BAF=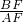
∴BF=AF•tan∠BAF=93×tan30°=93× ≈31×1.732=53.692(米)
≈31×1.732=53.692(米)
∴BE=BF+FE=BF+AD≈53.692+1.55=55.242≈55.24(米)
答:铁塔高BE约为55.24米.
分析:本题是一个直角梯形的问题,可以通过点A作AF⊥BE于点F,把求AB的问题转化求BF的长,从而可以在△ABF中利用三角函数.
点评:解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.
∵tan∠BAF=
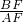
∴BF=AF•tan∠BAF=93×tan31°≈55.880(米)
∴BE=BF+FE=BF+AD≈55.880+1.55=57.430≈57.43(米)
答:铁塔高BE约长为57.43米.
(2)在Rt△ABF中,
∵tan∠BAF=
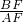
∴BF=AF•tan∠BAF=93×tan30°=93×
 ≈31×1.732=53.692(米)
≈31×1.732=53.692(米)∴BE=BF+FE=BF+AD≈53.692+1.55=55.242≈55.24(米)
答:铁塔高BE约为55.24米.
分析:本题是一个直角梯形的问题,可以通过点A作AF⊥BE于点F,把求AB的问题转化求BF的长,从而可以在△ABF中利用三角函数.
点评:解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
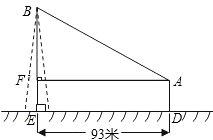 D=1.55米,请你解答以下两小题中的任意一个小题(若两个小题都做,按第(1)小题评分).
D=1.55米,请你解答以下两小题中的任意一个小题(若两个小题都做,按第(1)小题评分).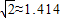 ,
,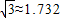 ).
).
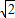 ≈1.414,
≈1.414,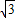 ≈1.732)
≈1.732)