题目内容
【题目】如图,在平面直角坐标系中,△ABO的边BO在x轴上,点A坐标(5,12),B(17,0),点C为BO边上一点,且AC=AO,点P为AB边上一点,且OP⊥AC.
(1)求出∠B的度数.
(2)试说明OA=OP.
(3)求点P的坐标及△PBO的面积.

【答案】(1)45°(2)详见解析(3)P(12,5),![]()
【解析】
(1) 过点A作AD⊥OB与点D,根据点A和点B坐标易知OD、AD、BD的长度,进而得到AD=BD,进而得到∠B的度数;
(2) 延长BA交y轴于点E,由已知可得∠AOC=∠ACO,由等角的余角相等可得∠EOA=∠POB,结合∠OEB=∠ABO=45°,由三角形外角定理可得∠OAP=∠OPA,进而可得OA=OP;
(3) 分别过点A作AM⊥y轴于点M,过点P作PN⊥x轴于点N,易知![]() ,进而可得AM=PN,OM=ON,根据点A和点B的坐标可得OM和AM的长度,进而可得ON和PN的长度,从而得到P点坐标和
,进而可得AM=PN,OM=ON,根据点A和点B的坐标可得OM和AM的长度,进而可得ON和PN的长度,从而得到P点坐标和![]() 的面积.
的面积.
(1)如图,过点A作AD⊥OB与点D,
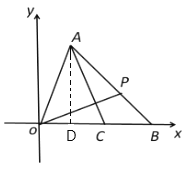
∵A(5,12),B(17,0),
∴OD=5,OB=17,AD=12,
∴BD=OB-OD=17-5=12,
∴AD=BD,
又∵AD⊥OB,
∴∠OBA=45°;
(2)如图,延长BA交y轴于点E,
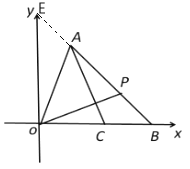
∵AO=AC,
∴∠AOC=∠ACO,
∵EO⊥OB,OP⊥AC,
∴∠AOC+∠EOA=90°,∠ACO+∠POB=90°,
∴∠EOA=∠POB,
∵EO⊥OB,∠ABO=45°,
∴∠OEB=∠ABO=45°,
∵∠OAP=∠OEA+∠EOA,∠OPA=∠POB+∠PBO,
∴∠OAP=∠OPA,
∴OA=OP.
(3)如图所示,分别过点A作AM⊥y轴于点M,过点P作PN⊥x轴于点N,
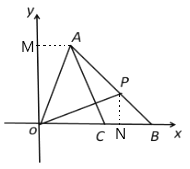
由(2)可知,OA=OP,∠MOA=∠PON,
又∵∠AMO=∠PNO=90°,
∴![]() ,
,
∴AM=PN,OM=ON,
∵点A坐标(5,12),点B坐标(17,0),
∴OM=12,AM=5,OB=17,
∴ON=OM=12,PN=AM=5,
∴点P坐标为(12,5),
![]() =
= ![]() =
= ![]() =
= ![]() .
.