题目内容
(2004•烟台)如图,已知在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.(1)如果M为AB上一点,且满足∠DMC=∠A,求AM的长;
(2)如果点M在AB边上移动(点M与A,B不重合),且满足∠DMN=∠A,MN交BC延长线于N,设AM=x,CN=y,求y关于x的函数解析式,并写出x的取值范围.

【答案】分析:(1)首先证明△ADM∽△MBC,根据相似比求得AN的长即可.
(2)据题中的思路可证得△ADM∽△BMN,据已知AM=x,CN=y及相似三角形相似比可得到y关于x的函数解析式.
解答: 解:在等腰梯形ABCD中,∵AB∥CD,
解:在等腰梯形ABCD中,∵AB∥CD,
∴∠A=∠B,
又∵∠A=∠DMC,∠1+∠2=∠3+∠DMC,
∴∠1=∠3,
∴△ADM∽△MBC,则 =
= ,AD=BC(已知),
,AD=BC(已知),
设AM=x,则 ,
,
∴x2-10x+9=0,∴x=1或x=9,
∴AM的长为1或9.

(2)同理可证△ADM∽△BMN,
可得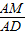 =
= 即
即 =
=
代入数值得y=-
 (0<x<1).
(0<x<1).
点评:本题主要考查相似三角形的判定及性质,涉及到二次函数知识点,考查学生综合知识的运用及综合解题的能力.
(2)据题中的思路可证得△ADM∽△BMN,据已知AM=x,CN=y及相似三角形相似比可得到y关于x的函数解析式.
解答:
 解:在等腰梯形ABCD中,∵AB∥CD,
解:在等腰梯形ABCD中,∵AB∥CD,∴∠A=∠B,
又∵∠A=∠DMC,∠1+∠2=∠3+∠DMC,
∴∠1=∠3,
∴△ADM∽△MBC,则
 =
= ,AD=BC(已知),
,AD=BC(已知),设AM=x,则
 ,
,∴x2-10x+9=0,∴x=1或x=9,
∴AM的长为1或9.

(2)同理可证△ADM∽△BMN,
可得
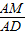 =
= 即
即 =
=
代入数值得y=-

 (0<x<1).
(0<x<1).点评:本题主要考查相似三角形的判定及性质,涉及到二次函数知识点,考查学生综合知识的运用及综合解题的能力.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 (2004•烟台)如图,现有两个边长为1:2的正方形ABCD与A′B′C′D′,已知B,C,B′,C′在同一直线上,且点C与点B′重合,请你利用这两个正方形,通过截割,平移,旋转的方法,拼出两个相似比为1:3的三角形.
(2004•烟台)如图,现有两个边长为1:2的正方形ABCD与A′B′C′D′,已知B,C,B′,C′在同一直线上,且点C与点B′重合,请你利用这两个正方形,通过截割,平移,旋转的方法,拼出两个相似比为1:3的三角形.

 直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,
直于x轴于N,直线CE切圆M于C,直线FG切圆M于F,交CE于G,已知点G的横坐标为3,