��Ŀ����
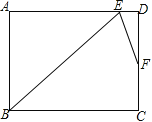
����Ŀ����ƽ��ֱ������ϵx0y��,����ͼ��G,������һ�������Φ�,��������ε�ij������x�ᴹֱ,��ͼ��G�ϵ����еĵ㶼�ڸ������ε��ڲ����߱���,��Ƹ������Φ�Ϊͼ��G��һ��������.����Ȼ,���ͼ��G����һ��������,��������������������,���ǽ�ͼ��G�������������б߳���С��һ��,��Ϊ���Ľ�����.��ͼ��ʾ,ͼ��GΪ�����߶κ�һ��Բ����ɵķ��ͼ��,ͼ�е����������ξ�Ϊͼ��G��������,����������ABCD����ͼ��G�Ľ�����.

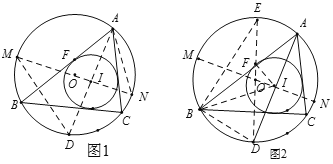
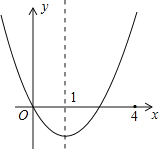
(1)���ڰ뾶Ϊ2�ġ�0,���Ľ����ǵı߳�Ϊ .
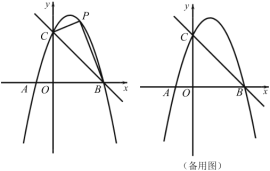
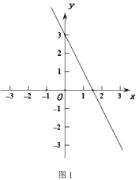
(2)��ͼ1,��PΪֱ��y=-2x+3��һ����,���߶�OP�Ľ����ǵı߳�Ϊ2,���P������;
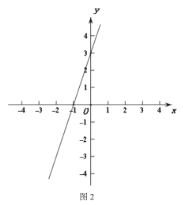
(3)��ͼ2,ֱ��y=3x+3��x��,y��ֱ���A,B,
����0ΪԲ��,rΪ�뾶�ġ�0���߶�AB�й�����,���ɡ�0���߶�AB��ɵ�ͼ��G�Ľ����ǵı߳�С��4,ֱ��д��r��ȡֵ��Χ;
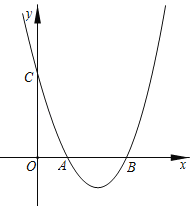
������������y=ax2+2ax-2(a��0)�ϴ��ڵ�C,ʹ�á�ABC�Ľ����ǵı߳�Ϊ3,ֱ��д��a��ȡֵ��Χ.
���𰸡���1��4��2��(![]() ,2)��(2,-1)��3��
,2)��(2,-1)��3��![]() ��a��
��a��![]() ��a<-2
��a<-2
��������
(1) �ɽ����ǵĶ���ɵñ߳�
��2���߶�OP�Ľ����ǵı߳�Ϊ2�����P������Ϊ(x,y)����|y|��|x|����|y|<|x|���ۿɵô�;
(3)�� rΪ�뾶�ġ�0���߶�AB�й�����,���ɡ�0���߶�AB��ɵ�ͼ��G�Ľ����ǵı߳�С��4�ɵô𰸣�
��4������������y= ax2+2ax-2 (a��0)�ϴ��ڵ�C,ʹ�á�ABC�Ľ����ǵı߳�Ϊ3���ɵô�.
(1)4;
(2)��:���P������Ϊ(x,y),���������
����|y|��|x|,���߶�OP�Ľ����ǵı߳�Ϊ|y|=2,
��y=2ʱ,-2x+3=2,��x=![]() ,��������,��PΪ(
,��������,��PΪ(![]() ,2);
,2);
��y=-2ʱ,-2x+3=-2,��x=-![]() ,����������,��ȥ.
,����������,��ȥ.
����|y|<|x|,���߶�OP�Ľ����ǵı߳�Ϊ|x|=2,
��x=2ʱ,y=-2x+3=-1,��������,��PΪ(2,-1);
��x=-2ʱ,y=-2x+3=7,����������,��ȥ.
����,��P������Ϊ(![]() ,2)��(2,-1)
,2)��(2,-1)
(3)��![]()
��a��![]() ��a<-2
��a<-2

����Ŀ�����±���ʾ����A��B��������
��1���� | ��2���� | ��3���� | ��4���� | ���� | ��9���� | ���� | ��n���� | |
A�� | ��6 | ��5 | ��2 | ���� | 58 | ���� | n2��2n��5 | |
B�� | 1 | 4 | 7 | 10 | ���� | 25 | ���� |
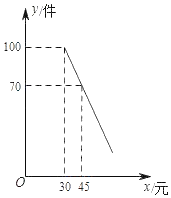
��1��A���4�������� ����
��2���ú�n�Ĵ���ʽ��ʾB���n�������� �������������ɣ�
��3�������������У��Ƿ����ͬһ���ϵ���������ȣ���˵����