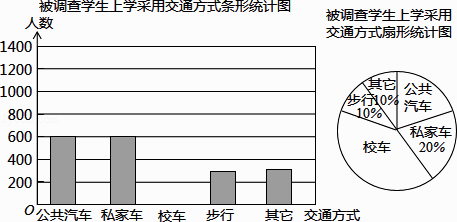
题目内容
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是( ) 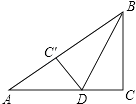
A.3cm2
B.4cm2
C.5cm2
D.6cm2
【答案】D
【解析】解:∵∠C=90°,BC=6cm,AC=8cm, ∴AB=10cm,
∵将△BCD沿BD折叠,使点C落在AB边的C′点,
∴△BCD≌△BC′D,
∴∠C=∠BC′D=90°,DC=DC′,BC=BC′=6cm,
∴AC′=AB﹣BC′=4cm,
设DC=xcm,则AD=(8﹣x)cm,
在Rt△ADC′中,AD2=AC′2+C′D2 ,
即(8﹣x)2=x2+42 , 解得x=3,
∵∠AC′D=90°,
∴△ADC′的面积═ ![]() ×AC′×C′D=
×AC′×C′D= ![]() ×4×3=6(cm2).
×4×3=6(cm2).
故选:D.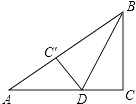
【考点精析】通过灵活运用勾股定理的概念和翻折变换(折叠问题),掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.

练习册系列答案
相关题目
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?