Question

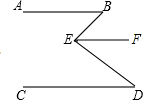如图，若AB∥EF∥CD，且∠B+∠BED+∠D=196°，∠B-∠D=22°，则∠BEF=

60°

．

Answer 1

分析：由“两直线平行，内错角相等”和等量代换求得2（∠B+∠D）=196°．结合已知条件∠B-∠D=22°，易求∠B=60°．故∠BEF=∠B=60°．

解答：解：如图，∵AB∥EF∥CD，
∴∠B=∠BEF，∠FED=∠D．
又∵∠B+∠BED+∠D=196°，∠BEF+∠FED=∠BED，
∴2（∠B+∠D）=196°．
∵∠B-∠D=22°，
∴∠B=60°，
∴∠BEF=∠B=60°．
故答案是：60°．

点评：本题考查了平行线的性质．两条平行线被第三条直线所截，内错角相等． 简单说成：两直线平行，内错角相等．