Question

【题目】等腰Rt△ABC中，∠BAC＝90°，AB＝AC,点A、点B分别是y轴、x轴上两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E；

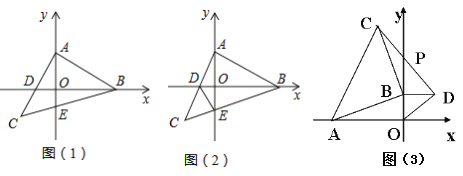
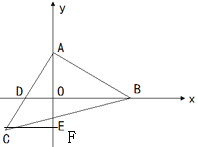
（1）如图（1），已知C点的横坐标为-1，直接写出点A的坐标；

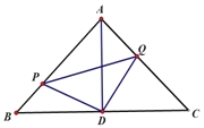
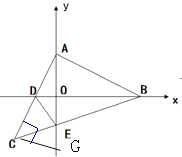
（2）如图（2）， 当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；

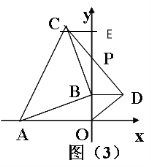
（3）如图（3）， 若点A在x轴上，且A（-4，0），点B在y轴的正半轴上运动时，分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连结CD交y轴于点P,问当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由，若不变化，请求出BP的长度.

Answer 1

【答案】（1）A（0，1）；（2）证明见解析；（3）BP的长度不变；理由见解析.

【解析】

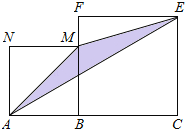
试题分析：（1）过点C作轴于点F，易证，∴CF＝OA＝1，∴A（0，1）；

（2）过点C作交y轴于点G，易证，则可得CG＝AD＝CD，由于∠ADB＝∠CGA，

∠DCE＝∠GCE＝45°，可证，则∠CDE＝∠AGC，∴∠ADB＝∠CDE；

（3）过点C作CE⊥y轴于点E，∵∠BAC＝90°，∴∠CBE+∠ABO＝90°，可证△CBE≌△BAO,∴CE＝BO,BE＝AO＝4,∵BD＝BO,∴CE＝BD.可证△CPE≌△DPB.∴BP＝EP＝2 .

试题解析：

（1）如图，过点C作轴于点F，易证（AAS），

∴CF＝OA＝1，

∴A（0，1）；

（2）如图，过点C作交y轴于点G，则（ASA），

∴CG＝AD＝CD，∠ADB＝∠CGA，

∵∠DCE＝∠GCE＝45°，

∴（SAS），

∴∠CDE＝∠AGC，

∴∠ADB＝∠CDE；

（4）BP的长度不变，理由如下：

过点C作CE⊥y轴于点E，

∵∠BAC＝90°，

∴∠CBE+∠ABO＝90°，

∵∠BAO+∠ABO＝90°，

∴∠CBE＝∠BAO.

∵∠CEB＝∠AOB＝90°,AB＝AC,

∴△CBE≌△BAO（AAS）,

∴CE＝BO,BE＝AO＝4,

∵BD＝BO,∴CE＝BD.

∵∠CEP＝∠DBP＝90°, ∠CPE＝∠DPB,

∴△CPE≌△DPB（AAS）.

∴BP＝EP＝2 .