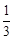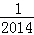题目内容
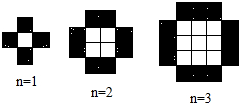
当n等于1,2,3…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形和黑色小正方形的个数总和等于 .(用n表示,n是正整数)

n2+4n
试题分析:观察不难发现,白色正方形的个数是相应序数的平方,黑色正方形的个数是相应序数的4倍,根据此规律写出即可.
第1个图形:白色正方形1个,黑色正方形4×1=4个,共有1+4=5个;
第2个图形:白色正方形22=4个,黑色正方形4×2=8个,共有4+8=12个;
第3个图形:白色正方形32=9个,黑色正方形4×3=12个,共有9+12=21个;
…,
第n个图形:白色正方形n2个,黑色正方形4n个,共有n2+4n个.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (k>0)和x轴上,若点B1(1,2),B2(3,4),且满足
(k>0)和x轴上,若点B1(1,2),B2(3,4),且满足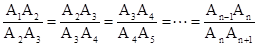 ,则直线
,则直线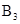 的坐标为 ,点
的坐标为 ,点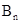 的坐标为_ .
的坐标为_ .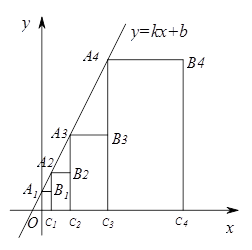
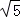
 的相反数是( )
的相反数是( )