题目内容
【题目】如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点M是BC的中点,作正方形MNPQ,使点A、C分别在MQ和MN上,连接AN、BQ.
(1)直接写出线段AN和BQ的数量关系是 .
(2)将正方形MNPQ绕点M逆时针方向旋转θ(0°<θ≤360°)
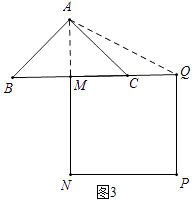
①判断(1)的结论是否成立?请利用图2证明你的结论;
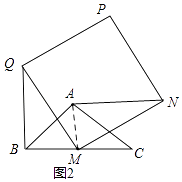
②若BC=MN=6,当θ(0°<θ≤360°)为何值时,AN取得最大值,请画出此时的图形,并直接写出AQ的值.
【答案】
(1)BQ=AN
(2)解:①BQ=AN成立.
理由:如图2,连接AM,
∵在Rt△BAC中,M为斜边BC中点,
∴AM=BM,AM⊥BC,
∴∠AMQ+∠QMB=90°.
∵四边形PQMN为正方形,
∴MQ=NM,且∠QMN=90°,
∴∠AMQ+∠NMA=90°,
∴∠BMQ=∠AMN.
在△BMQ和△AMN中,
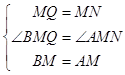 ,
,
∴△BMQ≌△AMN(SAS),
∴BQ=AN;
②由①得,BQ=AN,
∴当BQ取得最大值时,AN取得最大值.
如图3,当旋转角θ=270°时,BQ=AN(最大),此时∠AMQ=90°.
∵BC=MN=6,M是BC的中点,
∴MQ=6,AM= ![]() BC=3,
BC=3,
∴在Rt△AMQ中,由勾股定理得
AQ= ![]() =
= ![]() =3
=3 ![]() .
.
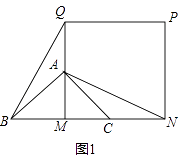
【解析】解:(1)BQ=AN.理由:如图1,∵△ABC是等腰直角三角形,∠BAC=90°,点M是BC的中点,
∴AM⊥BC,BM=AM,
∴∠AMB=∠AMC=90°.
∵四边形PQMN是正方形,
∴QM=NM.
在△QMB和△NMA中,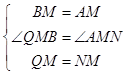 ,
,
∴△QMB≌△NMA(SAS),
∴BQ=AN.
所以答案是:BQ=AN;
【考点精析】关于本题考查的勾股定理的概念和正方形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案







