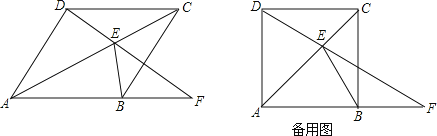
题目内容
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K,E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F. 
(1)求证:EF为⊙O的切线;
(2)若DK=2HK=AK,CH= ![]() ,求图中阴影部分的面积S.
,求图中阴影部分的面积S.
【答案】
(1)证明:连接OG,如图1所示:

∵弦CD⊥AB于点H,
∴∠AHK=90°,
∴∠HKA+∠KAH=90°,
∵EG=EK,
∴∠EGK=∠EKG,
∵∠HKA=∠GKE,
∴∠HAK+∠KGE=90°,
∵AO=GO,
∴∠OAG=∠OGA,
∴∠OGA+∠KGE=90°,
∴GO⊥EF,
∴EF是⊙O的切线
(2)解:∵CD⊥AB,
∴DH=CH= ![]() ,
,
∵DK=2HK=AK,
∴∠HAK=30°,HK= ![]() DH=
DH= ![]() ,
,
∴AH= ![]() HK=
HK= ![]() ,
,
连接OD,如图2所示:

设⊙O的半径为R,
在Rt△ODH中,由勾股定理得:( ![]() )2+(R﹣
)2+(R﹣ ![]() )2=R2,
)2=R2,
解得:R=2 ![]() ,
,
∴OH=OA﹣AH= ![]() =
= ![]() OD,
OD,
∴∠ODH=30°,△ODH的面积= ![]() OHDH=
OHDH= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
∴∠DOH=60°,
∴∠BOD=120°,
∴扇形OBGD的面积= ![]() =
= ![]() ,
,
∵OA=OG,
∴∠OGA=∠HAK=30°,
∴∠EGK=90°﹣30°=60°,
又∵EK=EG,
∴△GEK是等边三角形,
∴∠E=60°,
∴∠F=90°﹣60°=30°,
∵GO⊥EF,
∴OF=2OG=4 ![]() ,
,
∴HF=OH+OF=5 ![]() ,
,
∴HE= ![]() HF=
HF= ![]()
∴△EFH的面积= ![]() HFHE=
HFHE= ![]() ×5
×5 ![]() ×
× ![]() =
= ![]() ,
,
∴图中阴影部分的面积S= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]()
【解析】(1)连接OG,首先证明∠EGK=∠EKG,再证明∠HAK+∠KGE=90°,进而得到∠OGA+∠KGE=90°即GO⊥EF,进而证明EF是⊙O的切线;(2)与已知条件得出∠HAK=30°,HK= ![]() DH=
DH= ![]() ,AH=
,AH= ![]() HK=
HK= ![]() ,连接OD,设⊙O的半径为R,在Rt△ODH中,由勾股定理得出方程,解方程求出半径,得出OH=
,连接OD,设⊙O的半径为R,在Rt△ODH中,由勾股定理得出方程,解方程求出半径,得出OH= ![]() OD,求出∠ODH=30°,△ODH的面积=
OD,求出∠ODH=30°,△ODH的面积= ![]() ,再求出∠BOD=120°,得出扇形OBGD的面积=
,再求出∠BOD=120°,得出扇形OBGD的面积= ![]() ,证明△GEK是等边三角形,求出OF=2OG=4
,证明△GEK是等边三角形,求出OF=2OG=4 ![]() ,得出HF=OH+OF=5
,得出HF=OH+OF=5 ![]() ,求出HE=
,求出HE= ![]() ,计算出△EFH的面积,即可得出结果.
,计算出△EFH的面积,即可得出结果.
【考点精析】关于本题考查的垂径定理和扇形面积计算公式,需要了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能得出正确答案.