题目内容
已知锐角A满足关系式2sin2A-7sinA+3=0，则sinA的值为
- A.
- B.3
- C.或3
- D.4
A
分析：将sinA看做一个整体，采用换元思想解方程即可解答．
解答：设sinA=y，则上式可化为2y2-7y+3=0．
2y2-7y+3=（2y-1）（y-3）=0，
所以y1=3，y2=．
∵A为锐角，∴0＜sinA＜1，
故选A．
点评：此题要注意换元思想与锐角正弦值的求法，提高了学生的灵活应用能力．
分析：将sinA看做一个整体，采用换元思想解方程即可解答．
解答：设sinA=y，则上式可化为2y2-7y+3=0．
2y2-7y+3=（2y-1）（y-3）=0，
所以y1=3，y2=
．∵A为锐角，∴0＜sinA＜1，
故选A．
点评：此题要注意换元思想与锐角正弦值的求法，提高了学生的灵活应用能力．
练习册系列答案
相关题目
已知锐角A满足关系式2sin2A-7sinA+3=0，则sinA的值为（ ）
A、
| ||
| B、3 | ||
C、
| ||
| D、4 |
已知锐角A满足关系式2cos2A-7cosA+3=0，则cosA的值为（ ）
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
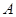满足关系式
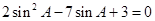，则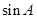
的值为（ ）
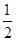B．3 C．