题目内容
(2001•呼和浩特)如图,图中的△BDC′是将矩形ABCD沿对角线BD折叠得到的,图中(包括实线,虚线在内)共有全等三角形( )对.
A.1
B.2
C.3
D.4
【答案】分析:共有四对,分别为△ABO≌△C′DO,△ABD≌△CDB,△ABD≌△C′DB,△CDB≌△C′DB.
解答:解:∵△BDC′是将矩形ABCD沿对角线BD折叠得到的
∴C′D=CD,∠C=∠C′,BD=BD
∴△CDB≌△C′DB
同理可证其它三对三角形全等.
故选D.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
解答:解:∵△BDC′是将矩形ABCD沿对角线BD折叠得到的
∴C′D=CD,∠C=∠C′,BD=BD
∴△CDB≌△C′DB
同理可证其它三对三角形全等.
故选D.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 的图象经过点(1,-1),则函数y=kx-2的图象不经过第( )象限.
的图象经过点(1,-1),则函数y=kx-2的图象不经过第( )象限. 的图象经过点(1,-1),则函数y=kx-2的图象不经过第( )象限.
的图象经过点(1,-1),则函数y=kx-2的图象不经过第( )象限.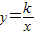 的图象经过点(1,-1),则函数y=kx-2的图象不经过第( )象限.
的图象经过点(1,-1),则函数y=kx-2的图象不经过第( )象限.