题目内容
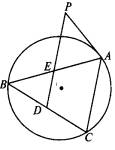
(浙江台州2003年中考试题)如图,PA是△ABC的外接圆O的切线,A是切点,PD∥AC,且PD与AB、BC分别相交于E、D.求证:(1)∠PAE=∠BDE;(2)EA·EB=ED·EP.
答案:
解析:
解析:
| 证明:(1)∵ PA是⊙O的切线,AB为⊙O的弦,
∴ ∠PAE=∠ACB. ∵ PD∥AC,∴ ∠ACB=∠BDE. ∴ ∠PAE=∠BDE. (2)由(1)知∠PAE=∠BDE, 又∵ ∠PEA=∠BED,∴ △PEA∽△BED. ∴ 点评:在圆中证角的相等,时常考虑弦切角、同弧或等弧所对的圆周角、圆内接四边形的外角等图形.必要时需运用等量代换转化为要证明的相等的角.
|

练习册系列答案
相关题目