题目内容
【题目】已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
(1)观察图形并找出一对全等三角形:△ ≌△ ,请加以证明;
(2)在(1)中你所找出的一对全等三角形,其中一个三角形可由另一个三角形经过怎样的变换得到?
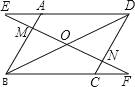
【答案】(1)△DOE≌△BOF;证明见解析(2)绕点O旋转180°后得到或以点O为中心作对称变换得到.
【解析】
试题分析:(1)本题要证明如△ODE≌△BOF,已知四边形ABCD是平行四边形,具备了同位角、内错角相等,又因为OD=OB,可根据AAS能判定△DOE≌△BOF;本题还可证明①△BOM≌△DON;②△ABD≌△CDB;
(2)平行四边形是中心对称图形,这三对全等三角形中的一个都是以其中另一个三角形绕点O旋转180°后得到或以点O为中心作对称变换得到.
试题解析:(1)△DOE≌△BOF;
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EDO=∠FBO,∠E=∠F.
又∵OD=OB,
∴△DOE≌△BOF(AAS).
①△BOM≌△DON.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∴∠MBO=∠NDO,∠BMO=∠DNO.
又∵BO=DO,
∴△BOM≌△DON(AAS).
②△ABD≌△CDB.
证明:∵四边形ABCD是平行四边形,
∴AD=CB,AB=CD.
又∵BD=DB,
∴△ABD≌△CDB(SSS).
(2)绕点O旋转180°后得到或以点O为中心作对称变换得到.

【题目】面对全球金融危机的挑战,我国政府毅然启动内需,改善民生.国务院决定从2009年2月1日起,“家电下乡”在全国范围内实施,农民购买人选产品,政府按原价购买总额的13%给予补贴返还.某村委会组织部分农民到商场购买人选的同一型号的冰箱、电视机两种家电,已知购买冰箱的数量是电视机的2倍,且按原价购买冰箱总额为40 000元、电视机总额为15 000元.根据“家电下乡”优惠政策,每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元,求冰箱、电视机各购买多少台?
(1)设购买电视机x台,依题意填充下列表格:
项目 家电种类 | 购买数量(台) | 原价购买总额(元) | 政府补贴返还比例(元) | 补贴返还总金额 | 每台补贴返还 金额(元) |
冰箱 | 40000 | 13% | |||
电视机 | x | 15000 | 13% |
(2)列出方程(组)并解答.
