题目内容
【题目】如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= ![]() (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1. 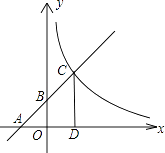
(1)求点A、B、D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)在x>0的条件下,根据图象说出反比例函数的值大于一次函数值的x的取值范围.
【答案】
(1)解:∵OA=OB=OD=1,
∴点A、B、D的坐标分别为A(﹣1,0),B(0,1),D(1,0)
(2)解:∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴ ![]() ,
,
解得 ![]() ,
,
∴一次函数的解析式为y=x+1.
∵点C在一次函数y=x+1的图象上,且CD⊥x轴,
∴点C的坐标为(1,2),
又∵点C在反比例函数y= ![]() (m≠0)的图象上,
(m≠0)的图象上,
∴m=2;
∴反比例函数的解析式为y= ![]()
(3)解:由函数的图象可知当0<x<1时反比例函数的值大于一次函数值
【解析】(1)根据OA=OB=OD=1和各坐标轴上的点的特点易得到所求点的坐标;(2)将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,由C点在一次函数的图象上可确定C点坐标,将C点坐标代入y= ![]() 可确定反比例函数的解析式.(3)由函数的图象即可得出反比例函数的值大于一次函数值的x的取值范围.
可确定反比例函数的解析式.(3)由函数的图象即可得出反比例函数的值大于一次函数值的x的取值范围.

 名校课堂系列答案
名校课堂系列答案【题目】某超市在“元旦”促销期间规定:超市内所有商品按标价的![]() 出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额 |
|
|
|
获得奖券金额(元) |
|
|
|
(符号![]() 表示
表示![]() 是大于或等于
是大于或等于![]() ,而小于
,而小于![]() 的数)
的数)
根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额![]() 商品的折扣
商品的折扣![]() 相应的奖券金额,例如:购买标价为
相应的奖券金额,例如:购买标价为![]() 元的商品,则消费金额为:
元的商品,则消费金额为: ![]() 元,获得的优惠额为:
元,获得的优惠额为: ![]() 元.
元.
(![]() )购买一件标价为
)购买一件标价为![]() 元的商品,求获得的优惠额.
元的商品,求获得的优惠额.
(![]() )对于标价在
)对于标价在![]() 元与
元与![]() 元之间(含
元之间(含![]() 元和
元和![]() 元)的商品,顾客购买标价为多少元的商品时可以得到
元)的商品,顾客购买标价为多少元的商品时可以得到![]() 的优惠率.(设购买该商品得到的优惠率
的优惠率.(设购买该商品得到的优惠率![]() 购买商品获得的优惠额
购买商品获得的优惠额![]() 商品的标价)
商品的标价)