题目内容
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,DA与⊙O相切于点A,DA=DC=![]() .
.

(1)求证:DC是⊙O的切线;
(2)若∠CAB=30°,求阴影部分的面积.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OC,证明OC⊥DC,即可得到DC是⊙O的切线;
(2)根据阴影部分的面积=扇形的面积-△BOC的面积计算即可.
试题解析:(1)证明:连接OC,
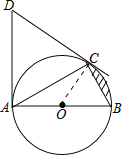
∵DA=DC,
∴∠DAC=∠DCA,
∵DA与⊙O相切于点A,
∴∠DAB=90°,
∴∠DAC+∠CAB=90°,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠DCA+∠ACO=90°,
即OC⊥DC,
∴DC是⊙O的切线;
(2)∵阴影部分的面积=扇形的面积-△BOC的面积,
∴阴影部分的面积=![]() .
.
考点:1.切线的判定与性质;2.扇形面积的计算.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】某校七年级为了解课堂发言情况,随机抽取了该年级部分学生,对他们某天在课堂上发言次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() 、
、![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图表中相关信息,回答下列问题:
,请结合图表中相关信息,回答下列问题:
组别 | 发言次数 |
|
|
|
|
|
|
|
|
|
|
|
|

(1)求出样本容量,并补全条形统计图;
(2)求![]() 组所在扇形的圆心角的度数;
组所在扇形的圆心角的度数;
(3)该年级共有学生800人,请你估计该年级在这天里发言次数不少于12的人数.