题目内容
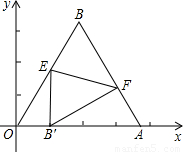
如图所示,△OAB是边长为2+| 3 |
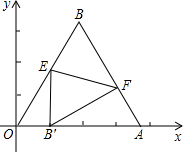 正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.
正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.(1)设OB′的长为x,△OB′E的周长为c,求c关于x的函数关系式;
(2)当B′E∥y轴时,求点B′和点E的坐标;
(3)当B′在OA上运动但不与O、A重合时,能否使△EB′F成为直角三角形?若能,请求出点B′的坐标;若不能,请说明理由.
分析:(1)根据折叠的性质可知BE=B′E,那么三角形OB′E的周长就等于OB′+OB,已知等边三角形OBA的边长,那么就可以表示出c与x的函数关系式了.
(2)当B′E∥y轴时,EB′⊥x轴,那么本题的关键就是求出直角三角形OB′E的两条直角边,可根据OE+EB′=2+
,而我们还可以通过∠EOB′的正弦函数得出OE,EB′的比例关系,然后根据这两个关系可得出OE,B′E的长,进而可求出OB′的长.也就得出了点B′和E点的坐标.
(3)要想使三角形EB′F是直角三角形,已知∠EB′F=60°,那么只有∠B′EF和∠B′FE为直角,当∠B′EF是直角时,那么∠AEF也是直角,那么A,E,B′在一条直线上,B′与O重合,那么与已知矛盾,因此不成立,同理可得出∠B′FE是直角的情况下也不成立,因此三角形EB′F不可能是直角三角形.
(2)当B′E∥y轴时,EB′⊥x轴,那么本题的关键就是求出直角三角形OB′E的两条直角边,可根据OE+EB′=2+
| 3 |
(3)要想使三角形EB′F是直角三角形,已知∠EB′F=60°,那么只有∠B′EF和∠B′FE为直角,当∠B′EF是直角时,那么∠AEF也是直角,那么A,E,B′在一条直线上,B′与O重合,那么与已知矛盾,因此不成立,同理可得出∠B′FE是直角的情况下也不成立,因此三角形EB′F不可能是直角三角形.
解答:解:(1)∵B′和B关于EF对称,
∴B′E=BE,
∴c=OB′+B′E+OE=OB′+BE+OE=x+OB=x+2+
.
(2)当B′E∥y轴时,∠EB′O=90°.
∵△OAB为等边三角形,
∴∠EOB′=60°,OB′=
EO.
设OB′=a,则OE=2a.
在Rt△OEB′中,tan∠EOB′=
,
∴B′E=B′Otan∠EOB′=
a;
∵B′E+OE=BE+OE=2+
,
∴a=1,
∴B′(1,0),E(1,
).
(3)答:不能.
理由如下:
∵∠EB′F=∠B=60°,
∴要使△EB′F成为直角三角形,则90°角只能是∠B′EF或∠B′FE.
假设∠B′EF=90°,
∵△FB′E与△FBE关于FE对称,
∴∠BEF=∠B′EF=90°,
∴∠BEB′=180°,
则B′、E、B三点在同一直线上,B′与O重合.
这与题设矛盾.
∴∠B′EF≠90°.
即△EB′F不能为直角三角形.
同理,∠B′FE=90°也不成立.
∴△EB′F不能成为直角三角形.
∴B′E=BE,
∴c=OB′+B′E+OE=OB′+BE+OE=x+OB=x+2+
| 3 |
(2)当B′E∥y轴时,∠EB′O=90°.
∵△OAB为等边三角形,
∴∠EOB′=60°,OB′=
| 1 |
| 2 |
设OB′=a,则OE=2a.
在Rt△OEB′中,tan∠EOB′=
| B′E |
| B′O |
∴B′E=B′Otan∠EOB′=
| 3 |
∵B′E+OE=BE+OE=2+
| 3 |
∴a=1,
∴B′(1,0),E(1,
| 3 |
(3)答:不能.
理由如下:
∵∠EB′F=∠B=60°,
∴要使△EB′F成为直角三角形,则90°角只能是∠B′EF或∠B′FE.
假设∠B′EF=90°,
∵△FB′E与△FBE关于FE对称,
∴∠BEF=∠B′EF=90°,
∴∠BEB′=180°,
则B′、E、B三点在同一直线上,B′与O重合.
这与题设矛盾.
∴∠B′EF≠90°.
即△EB′F不能为直角三角形.
同理,∠B′FE=90°也不成立.
∴△EB′F不能成为直角三角形.
点评:本题主要考查了折叠的性质,等边三角形的性质等知识点,根据折叠的性质得出线段和角相等是解题的关键.

练习册系列答案
相关题目
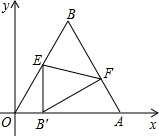 如图所示,△OAB是边长为
如图所示,△OAB是边长为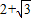 的等边三角形,其中O是坐标原点,顶点A在x轴的正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点A在x轴的正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.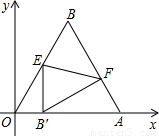
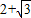 的等边三角形,其中O是坐标原点,顶点A在x轴的正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点A在x轴的正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.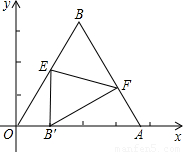
 的等边三角形,其中O是坐标原点,顶点A在x轴的正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点A在x轴的正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.