题目内容
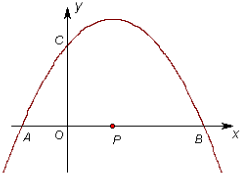 已知抛物线y=-ax2+2ax+b与x轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
已知抛物线y=-ax2+2ax+b与x轴的一个交点为A(-1,0),与y轴的正半轴交于点C.(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点B的坐标;
(2)当点C在以AB为直径的⊙P上时,求抛物线的解析式;
(3)坐标平面内是否存在点M,使得以点M和(2)中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
分析:(1)抛物线y=-ax2+2ax+b的对称轴,可以根据公式直接求出,抛物线与x轴的另一交点与A关于对称轴对称,因而交点就可以求出.
(2)AB的长度可以求出,连接PC,在直角三角形OCP中,根据勾股定理就可以求出C点的坐标,把这点的坐标代入抛物线的解析式,就可以求出解析式.
(3)本题应分AC或BC为对角线和以AB为对角线三种情况进行讨论,当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB.就可以求出点M的坐标.当以AB为对角线时,点M在x轴下方易证△AOC≌△BNM,可以求出点M的坐标.
(2)AB的长度可以求出,连接PC,在直角三角形OCP中,根据勾股定理就可以求出C点的坐标,把这点的坐标代入抛物线的解析式,就可以求出解析式.
(3)本题应分AC或BC为对角线和以AB为对角线三种情况进行讨论,当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB.就可以求出点M的坐标.当以AB为对角线时,点M在x轴下方易证△AOC≌△BNM,可以求出点M的坐标.
解答: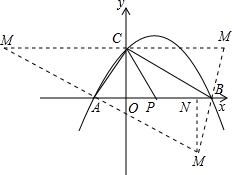 解:(1)对称轴是直线:x=1,点B的坐标是(3,0).(2分)
解:(1)对称轴是直线:x=1,点B的坐标是(3,0).(2分)
说明:每写对1个给(1分),“直线”两字没写不扣分.
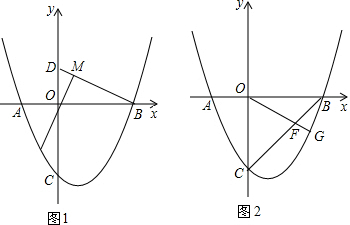
(2)如图,连接PC,
∵点A、B的坐标分别是A(-1,0)、B(3,0),
∴AB=4.
∴PC=
AB=
×4=2
在Rt△POC中,
∵OP=PA-OA=2-1=1,
∴OC=
=
,
∴b=
(3分)
当x=-1,y=0时,-a-2a+
=0
∴a=
(4分)
∴y=-
x2+
x+
.(5分)
(3)存在.(6分)理由:如图,连接AC、BC.
设点M的坐标为M(x,y).
①当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB.
由(2)知,AB=4,
∴|x|=4,y=OC=
.
∴x=±4.
∴点M的坐标为M(4,
)或(-4,
).(9分)
说明:少求一个点的坐标扣(1分).
②当以AB为对角线时,点M在x轴下方.
过M作MN⊥AB于N,则∠MNB=∠AOC=90度.
∵四边形AMBC是平行四边形,
∴AC=MB,且AC∥MB.
∴∠CAO=∠MBN.
∴△AOC≌△BNM.
∴BN=AO=1,MN=CO=
.
∵OB=3,
∴0N=3-1=2.
∴点M的坐标为M(2,-
).(12分)
综上所述,坐标平面内存在点M,使得以点A、B、C、M为顶点的四边形是平行四边形.
其坐标为M1(4,
),M2(-4,
),M3(2,-
).
说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分
 解:(1)对称轴是直线:x=1,点B的坐标是(3,0).(2分)
解:(1)对称轴是直线:x=1,点B的坐标是(3,0).(2分)说明:每写对1个给(1分),“直线”两字没写不扣分.
(2)如图,连接PC,
∵点A、B的坐标分别是A(-1,0)、B(3,0),
∴AB=4.
∴PC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△POC中,
∵OP=PA-OA=2-1=1,
∴OC=
| PC2-PO2 |
| 3 |
∴b=
| 3 |
当x=-1,y=0时,-a-2a+
| 3 |
∴a=
| ||
| 3 |
∴y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
(3)存在.(6分)理由:如图,连接AC、BC.
设点M的坐标为M(x,y).
①当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB.
由(2)知,AB=4,
∴|x|=4,y=OC=
| 3 |
∴x=±4.
∴点M的坐标为M(4,
| 3 |
| 3 |
说明:少求一个点的坐标扣(1分).
②当以AB为对角线时,点M在x轴下方.
过M作MN⊥AB于N,则∠MNB=∠AOC=90度.
∵四边形AMBC是平行四边形,
∴AC=MB,且AC∥MB.
∴∠CAO=∠MBN.
∴△AOC≌△BNM.
∴BN=AO=1,MN=CO=
| 3 |
∵OB=3,
∴0N=3-1=2.
∴点M的坐标为M(2,-
| 3 |
综上所述,坐标平面内存在点M,使得以点A、B、C、M为顶点的四边形是平行四边形.
其坐标为M1(4,
| 3 |
| 3 |
| 3 |
说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分
点评:本题主要考查了抛物线的轴对称性,是与勾股定理相结合的题目.难度较大.

练习册系列答案
相关题目
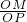 =
= ?若存在,求P点坐标;不存在,请说明理由.
?若存在,求P点坐标;不存在,请说明理由.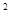 +bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,求:(1)抛物线解析式
+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,求:(1)抛物线解析式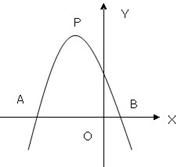
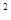 +bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,求:(1)抛物线解析式
+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,求:(1)抛物线解析式