题目内容
下列由已知得出的结论,不正确的是
- A.已知m=n,则ma=na
- B.已知
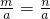 ,则m=n
,则m=n - C.已知m=n,则m+a2=n+a2
- D.已知ma=na,则m=n
D
分析:根据①等式的两边同时加上或减去同一个数或字母等式仍成立;②等式的两边同时乘以或除以同一个不为0的数或字母等式仍成立,可解决本题.
解答:A、根据等式性质2,m=n两边都乘以a,即可得到ma=na,正确;
B、根据等式性质2,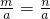 两边都乘以a,即可得到m=n,正确;
两边都乘以a,即可得到m=n,正确;
C、根据等式性质1,m=n两边都加a2,即可得到m+a2=n+a2,正确;
D、根据等式性质2,需条件a≠0,才可得到m=n,不正确;
故选D.
点评:本题主要考查等式的性质.需利用等式的性质对根据已知得到的等式进行变形,从而找到最后的答案.
分析:根据①等式的两边同时加上或减去同一个数或字母等式仍成立;②等式的两边同时乘以或除以同一个不为0的数或字母等式仍成立,可解决本题.
解答:A、根据等式性质2,m=n两边都乘以a,即可得到ma=na,正确;
B、根据等式性质2,
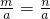 两边都乘以a,即可得到m=n,正确;
两边都乘以a,即可得到m=n,正确;C、根据等式性质1,m=n两边都加a2,即可得到m+a2=n+a2,正确;
D、根据等式性质2,需条件a≠0,才可得到m=n,不正确;
故选D.
点评:本题主要考查等式的性质.需利用等式的性质对根据已知得到的等式进行变形,从而找到最后的答案.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
下列由已知得出的结论,不正确的是( )
| A、已知m=n,则ma=na | ||||
B、已知
| ||||
| C、已知m=n,则m+a2=n+a2 | ||||
| D、已知ma=na,则m=n |
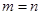 ,则
,则 B、已知
B、已知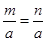 ,则
,则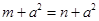 D、已知
D、已知 ,则
,则