��Ŀ����
Ϊ��Ԯ��ʧѧ��ͯ������ѧ��������2012��1�·ݿ�ʼ��ÿ��һ�ν�������������Ǯ�������в��ִ��Ĵ�����ڣ���ÿ6����һ�ν�������ڴ��һ���������������Ѳ��ƣ�����֪2�·ݴ�����㴢������д��80Ԫ��5�·ݴ�����㴢������д��125Ԫ��
��1��������2012��1�·ݴ��ǰ������������д�����Ԫ��
��2��Ϊ��ʵ�ֵ�2015��6�·ݴ�������������1000Ԫ��Ŀ�꣬�����ƻ���2013��1�·ݿ�ʼ��ÿ�´���2012��ÿ�´���tԪ��tΪ����������t����Сֵ��
��1��������2012��1�·ݴ��ǰ������������д�����Ԫ��
��2��Ϊ��ʵ�ֵ�2015��6�·ݴ�������������1000Ԫ��Ŀ�꣬�����ƻ���2013��1�·ݿ�ʼ��ÿ�´���2012��ÿ�´���tԪ��tΪ����������t����Сֵ��
��1��50Ԫ����2��11
�����������1��������ÿ�´��xԪ���������ԭ�д��yԪ�����ݡ�2�·ݴ�����㴢������д��80Ԫ��5�·ݴ�����㴢������д��125Ԫ�������з�������⣻
��2�����ɣ�1���������2012��Ĵ���������ݡ�2013��1�·ݺ�ÿ�´��루15+t��Ԫ��2013��1�µ�2015��6�¹���30���£�2015��6�·ݴ�������������1000Ԫ�������в���ʽ���.
��1��������ÿ�´��xԪ���������ԭ�д��yԪ���������
 �����
�����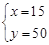
�𣺴������ԭ�д��50Ԫ��
��2���ɣ�1���ã�����2012�깲�д��12��15+50=230��Ԫ����
2013��1�·ݺ�ÿ�´��루15+t��Ԫ��
2013��1�µ�2015��6�¹���30���£�
������ã�230+30(15+t)>1000�����t >
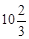 ��
������t����Сֵ��11��
����������Ĺؼ��Ƕ������⣬�ҵ�������ϵ�����ȹ�ϵ����ȷ�з�����Ͳ���ʽ���.

��ϰ��ϵ�д�
�����Ŀ
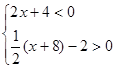 �������Ľ⼯�������ϱ�ʾ������
�������Ľ⼯�������ϱ�ʾ������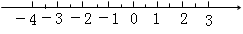
 �����������ϱ�ʾ�⼯
�����������ϱ�ʾ�⼯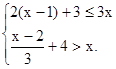 ��������.
��������. ��
�� �ķǸ�������ĸ���Ϊ
�ķǸ�������ĸ���Ϊ  ����
���� Ϊ����ʱ��������
Ϊ����ʱ�������� �Ľ�
�Ľ� Ϊ������
Ϊ������ Ϊ��������a��ֵΪ�� ��
Ϊ��������a��ֵΪ�� �� ������������_______________________.
������������_______________________. ������������ ��
������������ ��