题目内容
为发展山区农村经济,县政府鼓励农民结合本地实际开发果树种植.绿杨乡青年张青松种植了20棵苹果树,30棵桃树.按照种果树的经验,每棵苹果树结的果实的利润y1元与平均每棵苹果树的护理投资x元之间的关系是y1=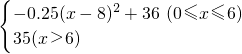 每棵桃树结的果实的利润y2元与平均每棵桃树的护理投资t元之间的关系是
每棵桃树结的果实的利润y2元与平均每棵桃树的护理投资t元之间的关系是 (0≤t≤6).青年张青松为这50棵果树总共投资240元.
(0≤t≤6).青年张青松为这50棵果树总共投资240元.
(1)求出张青松种植50棵果树的总利润w元与平均每棵苹果树护理投资x元之间的函数关系式,并指出x的取值范围;
(2)如何分配这两种果树的投资金额,使得张青松的总利润达到最大值?
解:(1)∵绿杨乡青年张青松种植了20棵苹果树,30棵桃树,平均每棵苹果树的护理投资x元,平均每棵桃树的护理投资t元,
∴20x+30t=240,∴t=8- x.
x.
则y2与x的关系是:y2=3t+27=-2x+51(3≤x≤12)
y2=45 (x<3).
∴当0≤x<3时,w=20y1+30y2=20[-0.25(x-8)2+36]+30×45=-5x2+80x+1750,
当3≤x≤6时,w=20y1+30y2=20[-0.25(x-8)2+36]+30(-2x+51)=-5x2+20x+1930,
当6<x≤12时,w=20y1+30y2=20×35+30(-2x+51)=-60x+2230.
即w与x之间的函数关系式是:
W=-5x2+80x+1750(0≤x<3)
W=-5x2+20x+1930 (3≤x≤6)
W=-60x+2230(6<x≤12).
(2)当0≤x<3时,w=-5x2+80x+1750=-5(x-8)2+2070,
w随x的增大而增大,
∴x<3时,w<1945.
当3≤x≤6时,w=-5x2+20x+1930=-5(x-2)2+1950,
w随x的增大而减小,
∴x=3时,wmax=-5+1950=1945.
当6<x≤12时,w=-60x+2230,-60<0,
w随x的增大而减小,
∴x>6时,w<-60×6+2230=1870.
综上所述,当x=3时,w有最大值,此时t=6.
即:每棵苹果树投资3元,每棵桃树投资6元时,可以使得张青松的总利润达到最大值.
分析:(1)利用绿杨乡青年张青松种植了20棵苹果树,30棵桃树,平均每棵苹果树的护理投资x元,平均每棵桃树的护理投资t元,
得出20x+30t=240,即t=8- x,进而得出y2与x的函数关系式,得出x的取值范围,进而得出w与x之间的关系式;
x,进而得出y2与x的函数关系式,得出x的取值范围,进而得出w与x之间的关系式;
(2)利用配方法以及二次函数的增减性分别求出最大值即可.
点评:此题主要考查了二次函数的应用以及二次函数求最值问题常用公式法或配方法,同学们需要掌握函数模型的选择与应用、基本不等式及函数的最值问题的灵活应用.
∴20x+30t=240,∴t=8-
 x.
x.则y2与x的关系是:y2=3t+27=-2x+51(3≤x≤12)
y2=45 (x<3).
∴当0≤x<3时,w=20y1+30y2=20[-0.25(x-8)2+36]+30×45=-5x2+80x+1750,
当3≤x≤6时,w=20y1+30y2=20[-0.25(x-8)2+36]+30(-2x+51)=-5x2+20x+1930,
当6<x≤12时,w=20y1+30y2=20×35+30(-2x+51)=-60x+2230.
即w与x之间的函数关系式是:
W=-5x2+80x+1750(0≤x<3)
W=-5x2+20x+1930 (3≤x≤6)
W=-60x+2230(6<x≤12).
(2)当0≤x<3时,w=-5x2+80x+1750=-5(x-8)2+2070,
w随x的增大而增大,
∴x<3时,w<1945.
当3≤x≤6时,w=-5x2+20x+1930=-5(x-2)2+1950,
w随x的增大而减小,
∴x=3时,wmax=-5+1950=1945.
当6<x≤12时,w=-60x+2230,-60<0,
w随x的增大而减小,
∴x>6时,w<-60×6+2230=1870.
综上所述,当x=3时,w有最大值,此时t=6.
即:每棵苹果树投资3元,每棵桃树投资6元时,可以使得张青松的总利润达到最大值.
分析:(1)利用绿杨乡青年张青松种植了20棵苹果树,30棵桃树,平均每棵苹果树的护理投资x元,平均每棵桃树的护理投资t元,
得出20x+30t=240,即t=8-
 x,进而得出y2与x的函数关系式,得出x的取值范围,进而得出w与x之间的关系式;
x,进而得出y2与x的函数关系式,得出x的取值范围,进而得出w与x之间的关系式;(2)利用配方法以及二次函数的增减性分别求出最大值即可.
点评:此题主要考查了二次函数的应用以及二次函数求最值问题常用公式法或配方法,同学们需要掌握函数模型的选择与应用、基本不等式及函数的最值问题的灵活应用.

练习册系列答案
相关题目
 每棵桃树结的果实的利润y2元与平均每棵桃树的护理投资t元之间的关系是
每棵桃树结的果实的利润y2元与平均每棵桃树的护理投资t元之间的关系是 (0≤t≤6).青年张青松为这50棵果树总共投资240元.
(0≤t≤6).青年张青松为这50棵果树总共投资240元.