题目内容
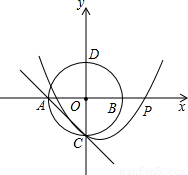
(2005•山西)如图,在平面直角坐标系xOy,半径为1的⊙O分别交x轴、y轴于A、B、C、D四点,抛物线y=x2+bx+c经过点C且与直线AC只有一个公共点.(1)求直线AC的解析式;
(2)求抛物线y=x2+bx+c的解析式;
(3)点P为(2)中抛物线上的点,由点P作x轴的垂线,垂足为点Q,问:此抛物线上是否存在这样的点P,使△PQB∽△ADB?若存在,求出P点坐标;若不存在,请说明理由.
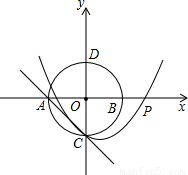
【答案】分析:(1)因为⊙O的半径为1,所以可知A、B、C、D四点的坐标,根据A、C两点的坐标用待定系数法即可求出直线AC的解析式.
(2)因为C点坐标为(0,-1),抛物线过C点,所以c=-1,将y=-x-1代入解析式y=x2+bx-1得x2+(b+1)x=0,因为抛物线与直线只有一个交点,故判别式△=0,可求得b的值;
(3)假设存在符合条件的点P,根据相似三角形的性质,判断出PQ=QB,列出关于P点坐标的表达式,即可解答.
解答: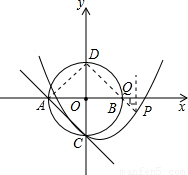 解:(1)由题意可知A(-1,0),B(1,0),C(0,-1),D(0,1),
解:(1)由题意可知A(-1,0),B(1,0),C(0,-1),D(0,1),
设过A、C两点的直线解析式为y=kx+b(k≠0),
把A(-1,0),C(0,-1)代入得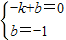 ,
,
解得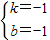 ,
,
故直线AC的解析式为y=-x-1;
(2)∵抛物线过C(0,-1),
∴x2+(b+1)x=0,
∵直线AC与抛物线只有一个公共点C,
∴方程x2+(b+1)x=O有两个相等实数根,
即△=0,
∴b1=b2=-1,
∴抛物线解析式为y=x2-x-1;
(3)假设存在符合条件的点P,
设P点坐标为(a,a2-a-1),则Q(a,0),
∵△ADB为等腰直角三角形,△PQB∽△ADB,
∴△PQB为等腰直角三角形,又PQ⊥QB,
∴PQ=QB即|a2-a-1|=|a-1|,
当a2-a-1=a-1时,
解得:a1=0,a2=2;
当a2-a-1=-(a-1)时,
解得:a3=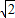 ,a4=-
,a4=-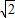 ,
,
∴a1=0,a2=2,a3=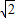 ,a4=-
,a4=- ,
,
∴存在符合条件的点P,共有四个,
分别为P1(O,-1)、P2(2,1)、P3(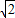 ,1-
,1-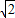 )、P4(-
)、P4(-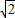 ,1+
,1+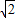 ).
).
点评:此题将二次函数、一次函数和圆的相关知识相结合,考查了用待定系数法求函数解析式、函数图象交点个数与函数解析式组成的方程组解的个数的关系以及点的存在性问题,有一定的开放性.
(2)因为C点坐标为(0,-1),抛物线过C点,所以c=-1,将y=-x-1代入解析式y=x2+bx-1得x2+(b+1)x=0,因为抛物线与直线只有一个交点,故判别式△=0,可求得b的值;
(3)假设存在符合条件的点P,根据相似三角形的性质,判断出PQ=QB,列出关于P点坐标的表达式,即可解答.
解答:
 解:(1)由题意可知A(-1,0),B(1,0),C(0,-1),D(0,1),
解:(1)由题意可知A(-1,0),B(1,0),C(0,-1),D(0,1),设过A、C两点的直线解析式为y=kx+b(k≠0),
把A(-1,0),C(0,-1)代入得
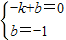 ,
,解得
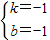 ,
,故直线AC的解析式为y=-x-1;
(2)∵抛物线过C(0,-1),
∴x2+(b+1)x=0,
∵直线AC与抛物线只有一个公共点C,
∴方程x2+(b+1)x=O有两个相等实数根,
即△=0,
∴b1=b2=-1,
∴抛物线解析式为y=x2-x-1;
(3)假设存在符合条件的点P,
设P点坐标为(a,a2-a-1),则Q(a,0),
∵△ADB为等腰直角三角形,△PQB∽△ADB,
∴△PQB为等腰直角三角形,又PQ⊥QB,
∴PQ=QB即|a2-a-1|=|a-1|,
当a2-a-1=a-1时,
解得:a1=0,a2=2;
当a2-a-1=-(a-1)时,
解得:a3=
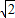 ,a4=-
,a4=-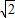 ,
,∴a1=0,a2=2,a3=
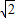 ,a4=-
,a4=- ,
,∴存在符合条件的点P,共有四个,
分别为P1(O,-1)、P2(2,1)、P3(
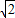 ,1-
,1-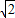 )、P4(-
)、P4(-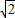 ,1+
,1+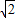 ).
).点评:此题将二次函数、一次函数和圆的相关知识相结合,考查了用待定系数法求函数解析式、函数图象交点个数与函数解析式组成的方程组解的个数的关系以及点的存在性问题,有一定的开放性.

练习册系列答案
相关题目