题目内容
【题目】如图，四边形OMTN中，OM=ON，TM=TN，我们把这种两组邻边分别相等的四边形叫做筝形．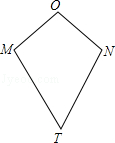
（1）探究筝形对角线之间的位置关系，并证明你的结论；
（2）在筝形ABCD中，已知AB=AD=10，BC=CD，BC＞AB，BD、AC为对角线，BD=16．
①若∠ABC=90°，求AC的长；
②过点B作BF⊥CD于F，BF交AC于点E，连接DE．当四边形ABED为菱形时，求点F到AB的距离．
【答案】
（1）
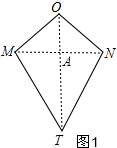
解：如图1，连接MN、OT交于点A，
MN⊥OT，理由是：
∵OM=ON，TM=TN，OT=OT，
∴△OMT≌△ONT，
∴∠MOT=∠NOT，
∵OM=ON，
∴MN⊥OT
（2）
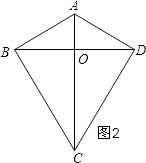
解：①如图2所示，
∵四边形ABCD为筝形，
∴AC⊥BD，
∵AB=AD，
∴OB=OD= 
BD= ×16=8，
由勾股定理得：AO= 
=6，
设OC=x，
∵∠ABC=90°，
∴BC2=AC2﹣AB2，BC2=OC2+OB2，
∴82+x2=（6+x）2﹣102，
解得：x= 
，
∴AC=OA+OC=6+ = 
；
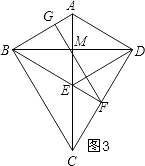
②如图3所示：
∵四边形ABED为菱形，
∴BE=AD=10，EM=AM=6，
∵∠FBD=∠FBD，∠BMC=∠BFD=90°，
∴△BEM∽△BDF，
∴ 
，
∴ 
，
∴DF=9.6，
在Rt△DEF中，EF= 
=2.8，
∴BF=2.8+10=12.8，
∵∠BGF=∠EFD=90°，∠GBF=∠FED，
∴△BGF∽△EFD，
∴ 
，
∴FG= 
= 
=12.288．
则点F到AB的距离为12.288
【解析】（1）如图1，证明△OMT≌△ONT，得∠MOT=∠NOT，再根据等腰△OMN三线合一的性质得MN⊥OT；（2）①如图2，先根据勾股定理求AO的长，再利用勾股定理列方程求OC的长，则AC=OC+AO，代入得出结论；②如图3，先证明△BEM∽△BDF，可得 ，求出DF=9.6；再通过勾股定理求EF的长，则得BF的长，通过证明△BGF∽△EFD，得 ，所以可以求FG的长，即点F到AB的距离．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
