Question

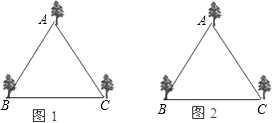某公园有一个边长为4米的正三角形花坛，三角形的顶点A、B、C上各有一棵古树．现决定把原来的花坛扩建成一个圆形或平行四边形花坛，要求三棵古树不能移动，且三棵古树位于圆周上或平行四边形的顶点上．以下设计过程中画图工具不限．
（1）按圆形设计，利用图1画出你所设计的圆形花坛示意图；
（2）按平行四边形设计，利用图2画出你所设计的平行四边形花坛示意图；
（3）若想新建的花坛面积较大，选择以上哪一种方案合适？请说明理由．

Answer 1

分析：（1）过A、B、C作圆即可，具体作法是：分别作AB、BC的垂直平分线，两线交于点O，以O为圆心，OA长为半径即可作圆；
（2）分别过A、C作BC、AB的平行线，两线交于点D，平行四边形ABCD即为所求；
（3）连接AO并延长交BC于D．可知AD是等边三角形的高，连接OB，在直角三角形OBD中，利用BD=0.5BC=2，∠OBD=30度，结合三角函数，求出半径和圆的面积，而平行四边形的面积等于三角形ABC面积的2倍，比较即可求出答案．

解答：解：
（1）（2）
；

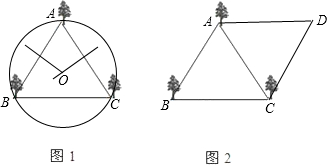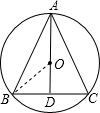
（3）连接OB，OA，并延长AO交BC于D，
∵r=OB=

BD

cos30°

=

4

3

3

，
∴S_⊙O=πr²=

16π

3

≈16.75，
又S_{平行四边形}=2S_△ABC=2×

1

2

×4²×sin60°=8

3

≈13.86，
∵S_⊙O＞S_{平行四边形}，
∴选择建圆形花坛面积较大．

点评：本题需利用圆的有关知识结合三角函数解决问题．