题目内容
2012年6月5日是第40个世界环境日,世界环境日的主题为“多个物种、一颗星球、一个未来”。为了响应节能减排的号召,某品牌汽车店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共16辆,以满足广大支持环保的购车者的需求。市场营销人员经过市场调查得到如下信息:
(1)若经营者的购买资金不少于576万元且不多于600万元,有哪几种进车方案?
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你作为一名购车者,将会选购哪一种型号的汽车?并说明理由。
| | 成本价(万元/辆) | 售价(万元/辆) |
| A型 | 30 | 32 |
| B型 | 42 | 45 |
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你作为一名购车者,将会选购哪一种型号的汽车?并说明理由。
设A型汽车购进x辆,则B型汽车购进(16-x)辆。
 根据题意得: 30x+42(16-x)≤600
根据题意得: 30x+42(16-x)≤600
30x+42(16-x)≥576
解得:6≤x≤8.∵x为整数
∴x取6、7、8。
∴有三种购进方案:
(2)设总利润为w万元,
根据题意得:W=(32-30)x+(45-42)(16-x)
=-x+48
∵k=-1<0
∴w随x的增大而减小
∴当x=6时,w有最大值,w最大=-6+48=42(万元)
∴当购进A型车6辆,B型车10辆时,可获得最大利润,最大利润是42万元。
(3)设电动汽车行驶的里程为a万公里。
当32+0.65a=45时,a=20<30
∴选购太阳能汽车比较合算
 根据题意得: 30x+42(16-x)≤600
根据题意得: 30x+42(16-x)≤60030x+42(16-x)≥576
解得:6≤x≤8.∵x为整数
∴x取6、7、8。
∴有三种购进方案:
| A型 | 6辆 | 7辆 | 8辆 |
| B型 | 10辆 | 9辆 | 8辆 |
(2)设总利润为w万元,
根据题意得:W=(32-30)x+(45-42)(16-x)
=-x+48
∵k=-1<0
∴w随x的增大而减小
∴当x=6时,w有最大值,w最大=-6+48=42(万元)
∴当购进A型车6辆,B型车10辆时,可获得最大利润,最大利润是42万元。
(3)设电动汽车行驶的里程为a万公里。
当32+0.65a=45时,a=20<30
∴选购太阳能汽车比较合算
(1)根据已知信息和若经营者的购买资金不少于576万元且不多于600万元,列出不等式组,求解得出进车方案.
(2)根据已知列出利润函数式,求最值,选择方案.
(3)根据已知通过计算分析得出答案.
(2)根据已知列出利润函数式,求最值,选择方案.
(3)根据已知通过计算分析得出答案.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 x3ya+b的和是单项式,那么这两个单项式的积是( )
x3ya+b的和是单项式,那么这两个单项式的积是( ) x3y2
x3y2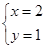 的二元一次方程组:___________.
的二元一次方程组:___________. 的解是
的解是 ,则
,则 的值是
的值是  的解集为 .( )
的解集为 .( )



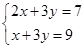 ,①-②得【 ▲ 】
,①-②得【 ▲ 】


