题目内容
(2012•玉林)如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A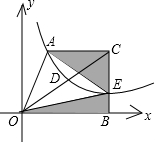 的双曲线y=
的双曲线y=
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
(1)填空:双曲线的另一支在第
(2)若点C的坐标为(2,2),当点E在什么位置时,阴影部分的面积S最小?
(3)若
=
,S△OAC=2,求双曲线的解析式.
 的双曲线y=
的双曲线y=| k |
| x |
(1)填空:双曲线的另一支在第
三
三
象限,k的取值范围是k>0
k>0
;(2)若点C的坐标为(2,2),当点E在什么位置时,阴影部分的面积S最小?
(3)若
| OD |
| OC |
| 1 |
| 2 |
分析:(1)根据反比例函数图象与性质得到:双曲线y=
的一支在第一象限,则k>0,得到另一支在第三象限;
(2)根据梯形的性质,AC∥x轴,BC⊥x轴,而点C的坐标为(2,2),则A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),再分别把y=2或x=2代入y=
可得到A点的坐标为(
,2),E点的坐标为(2,
),然后计算S阴影部分=S△ACE+S△OBE=
×(2-
)×(2-
)+
×2×
=
k2-
k+2,配方得
(k-2)2+
,当k=2时,S阴影部分最小值为
,则E点的坐标为(2,1),即E点为BC的中点;
(3)设D点坐标为(a,
),由
=
,则OD=DC,即D点为OC的中点,于是C点坐标为(2a,
),得到A点的纵坐标为
,把y=
代入y=
得x=
,确定A点坐标为(
,
),根据三角形面积公式由S△OAC=2得到
×(2a-
)×
=2,然后解方程即可求出k的值.
| k |
| x |
(2)根据梯形的性质,AC∥x轴,BC⊥x轴,而点C的坐标为(2,2),则A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),再分别把y=2或x=2代入y=
| k |
| x |
| k |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)设D点坐标为(a,
| k |
| a |
| OD |
| OC |
| 1 |
| 2 |
| 2k |
| a |
| 2k |
| a |
| 2k |
| a |
| k |
| x |
| a |
| 2 |
| a |
| 2 |
| 2k |
| a |
| 1 |
| 2 |
| a |
| 2 |
| 2k |
| a |
解答:解:(1)三,k>0;
(2)∵梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,
而点C的坐标为(2,2),
∴A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),
把y=2代入y=
得x=
;把x=2代入y=
得y=
,
∴A点的坐标为(
,2),E点的坐标为(2,
),
∴S阴影部分=S△ACE+S△OBE
=
×(2-
)×(2-
)+
×2×
=
k2-
k+2
=
(k-2)2+
,
当k-2=0,即k=2时,S阴影部分最小,最小值为
;
∴E点的坐标为(2,1),即E点为BC的中点,
∴当点E在BC的中点时,阴影部分的面积S最小;
(3)设D点坐标为(a,
),
∵
=
,
∴OD=DC,即D点为OC的中点,
∴C点坐标为(2a,
),
∴A点的纵坐标为
,
把y=
代入y=
得x=
,
∴A点坐标为(
,
),
∵S△OAC=2,
∴
×(2a-
)×
=2,
∴k=
,
∴双曲线的解析式为y=
.
(2)∵梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,
而点C的坐标为(2,2),
∴A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),
把y=2代入y=
| k |
| x |
| k |
| 2 |
| k |
| x |
| k |
| 2 |
∴A点的坐标为(
| k |
| 2 |
| k |
| 2 |
∴S阴影部分=S△ACE+S△OBE
=
| 1 |
| 2 |
| k |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
=
| 1 |
| 8 |
| 1 |
| 2 |
=
| 1 |
| 8 |
| 3 |
| 2 |
当k-2=0,即k=2时,S阴影部分最小,最小值为
| 3 |
| 2 |
∴E点的坐标为(2,1),即E点为BC的中点,
∴当点E在BC的中点时,阴影部分的面积S最小;
(3)设D点坐标为(a,
| k |
| a |
∵
| OD |
| OC |
| 1 |
| 2 |
∴OD=DC,即D点为OC的中点,
∴C点坐标为(2a,
| 2k |
| a |
∴A点的纵坐标为
| 2k |
| a |
把y=
| 2k |
| a |
| k |
| x |
| a |
| 2 |
∴A点坐标为(
| a |
| 2 |
| 2k |
| a |
∵S△OAC=2,
∴
| 1 |
| 2 |
| a |
| 2 |
| 2k |
| a |
∴k=
| 4 |
| 3 |
∴双曲线的解析式为y=
| 4 |
| 3x |
点评:本题考查了反比例函数综合题:当k>0时,反比例函数y=
(k≠0)的图象分布在第一、三象限;点在反比例函数图象上,则点的横纵坐标满足图象的解析式;运用梯形的性质得到平行线段,从而找到点的坐标特点.
| k |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
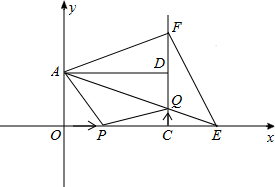 (2012•玉林)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2
(2012•玉林)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2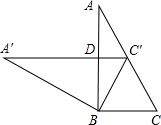 (2012•玉林)如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D=
(2012•玉林)如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D=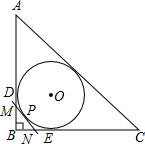 (2012•玉林)如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧
(2012•玉林)如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧
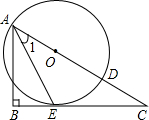 (2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.