题目内容
2010年的春天，某地旱情严重，若该地10号、15号的人日均用水量分别为18千克和15千克，并一直按此趋势直线下降．当人日均用水量低于10千克时，政府将向当地居民送水．那么政府就开始送水的日期为________号．
24
分析：根据题目说明，我们可知该地的用水量与用水的日期满足一次函数关系式，因而设该地用水的日期为x号，日均用水量为y千克，则关系式为y=kx+b．根据该地10号、15号的人日均用水量分别为18千克和15千克，可得该一次函数图象上的两点（10，18）、（15，15）．将这两点代入关系式，解得k、b的值，那么该一次函数关系式就确定了．根据y=10，确定出x的取值，又根据日期的实际情况，只能取整数．那么即可确定政府开始送水的日期．
解答：设该地用水的日期为x号，日均用水量为y千克，
用水量与用水的日期满足关系式：y=kx+b，
则由题意得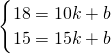
，
解得k=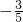
，b=24，
即该关系式为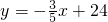
，
当y=10时，则x=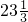
，
即政府开始送水的日期为24号．
故答案为24．
点评：本题主要考查用待定系数法求一次函数关系式，并会用一次函数研究实际问题，具备在直角坐标系中的读图能力．
分析：根据题目说明，我们可知该地的用水量与用水的日期满足一次函数关系式，因而设该地用水的日期为x号，日均用水量为y千克，则关系式为y=kx+b．根据该地10号、15号的人日均用水量分别为18千克和15千克，可得该一次函数图象上的两点（10，18）、（15，15）．将这两点代入关系式，解得k、b的值，那么该一次函数关系式就确定了．根据y=10，确定出x的取值，又根据日期的实际情况，只能取整数．那么即可确定政府开始送水的日期．
解答：设该地用水的日期为x号，日均用水量为y千克，
用水量与用水的日期满足关系式：y=kx+b，
则由题意得
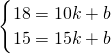，解得k=
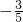，b=24，即该关系式为
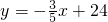，当y=10时，则x=
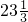，即政府开始送水的日期为24号．
故答案为24．
点评：本题主要考查用待定系数法求一次函数关系式，并会用一次函数研究实际问题，具备在直角坐标系中的读图能力．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
的一个交点是（a，1），求一次函数的解析式以及另一个交点坐标．
sin60°-sin30°-2tan 45°
与y=kx（k≠0）的图象有两个交点；
．
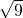的结果是________．