题目内容
 如图,边长为a的正方形ABCD的四边贴着直线l向右无滑动“滚动”,当正方形“滚动”一周时,该正方形的中心O经过的路程是多少?顶点A经过的路程又是多少?
如图,边长为a的正方形ABCD的四边贴着直线l向右无滑动“滚动”,当正方形“滚动”一周时,该正方形的中心O经过的路程是多少?顶点A经过的路程又是多少?分析:(1)根据题意,画出正方形ABCD“滚动”一周后中心O所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程;
(2)根据题意,画出正方形ABCD“滚动”一周后顶点A所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程.
(2)根据题意,画出正方形ABCD“滚动”一周后顶点A所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程.
解答:解:(1)

如图1,正方形ABCD“滚动”一周时,中心O所经过的路程为:
L中=
×2π(
a)×4(8分)
=
πa.(10分)
(2)
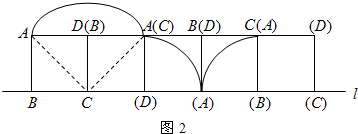
如图2,正方形ABCD“滚动”一周时,顶点A所经过的路程为:
L顶=
×2π(
a)+2×
×2πa(18分)
=
×2
πa+2×
×2πa=
πa.(20分)

如图1,正方形ABCD“滚动”一周时,中心O所经过的路程为:
L中=
| 1 |
| 4 |
| ||
| 2 |
=
| 2 |
(2)

如图2,正方形ABCD“滚动”一周时,顶点A所经过的路程为:
L顶=
| 1 |
| 4 |
| 2 |
| 1 |
| 4 |
=
| 1 |
| 4 |
| 2 |
| 1 |
| 4 |
2+
| ||
| 2 |
点评:本题考查了弧长的计算、正方形的性质.在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=n°πR÷180°.

练习册系列答案
相关题目

 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P. 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
