题目内容
如图,已知平面直角坐标系中三个点A(-8,0)、B(2,0)、C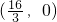 ,
,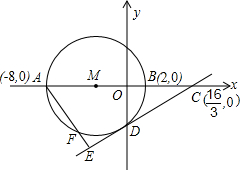 O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
O为坐标原点.以AB为直径的⊙M与y轴的负半轴交于点D.
(1)求直线CD的解析式;
(2)求证:直线CD是⊙M的切线;
(3)过点A作AE⊥CD,垂足为E,且AE与⊙M相交于点F,求一个一元二次方程,使它的两个根分别是AE和AF.
(1)解:∵A(-8,0),B(2,0),
∴⊙M的圆心为(-3,0),且⊙M的半径为5.
连接MD.
在Rt△OMD中,
OD=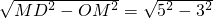 =4,
=4,
∴D(0,-4).
设所求直线CD的解析式为y=kx+b,则由C( ,0)、D(0,-4)两点,
,0)、D(0,-4)两点,
得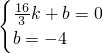 ,
,
解得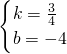 .
.
故所求直线CD的解析式为y= x-4.
x-4.
(2)证明:在Rt△CDO中,CD2=OD2+OC2=42+( )2=
)2=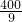 .
.
在△CDM中,MC=3+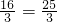 ,DM=5,
,DM=5,
∴DM2+CD2=25+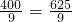 .
.
又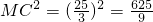 ,
,
∴MD2+CD2=MC2.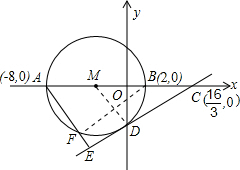
∴△CDM是直角三角形,且
∠MDC=90°,CD经过半径MD的外端点D,
∴直线CD是⊙M的切线.
(3)解:由已知,AE⊥CD,由(2),MD⊥CD,
∴MD∥AE,
∴△CDM∽△CEA.
∴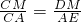 ,即
,即 ,解得AE=8.
,解得AE=8.
连接BF.则∠AFB=90°.
又∠MDC=90°,∠CMD=∠CAE,
∴Rt△CDM∽Rt△BFA.
∴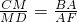 ,即
,即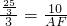 ,解得AF=6.
,解得AF=6.
故所求的一个一元二次方程是x2-14x+48=0.
分析:(1)已知A、B的坐标就可以求出直径AB的长,弦心距MB的长,根据垂径定理就可以求出BD的长,即得到D的坐标.根据待定系数法就可以求出CD的解析式.
(2)连接MD,根据M,C,D的坐标就可以得△CDM的三边的长,根据勾股定理的逆定理证明三角形是直角三角形.
(3)易证△CDM∽△CEA,根据相似三角形的对应边的比相等,可以求出AE,再证明Rt△CDM∽Rt△BFA,就可以得到AF,则所求的一元二次方程就可以得到.
点评:本题主要考查了待定系数法求函数解析式,以及相似三角形的性质,相似三角形的对应边的比相等.
∴⊙M的圆心为(-3,0),且⊙M的半径为5.
连接MD.
在Rt△OMD中,
OD=
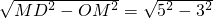 =4,
=4,∴D(0,-4).
设所求直线CD的解析式为y=kx+b,则由C(
 ,0)、D(0,-4)两点,
,0)、D(0,-4)两点,得
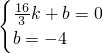 ,
,解得
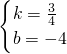 .
.故所求直线CD的解析式为y=
 x-4.
x-4. (2)证明:在Rt△CDO中,CD2=OD2+OC2=42+(
 )2=
)2=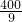 .
.在△CDM中,MC=3+
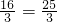 ,DM=5,
,DM=5,∴DM2+CD2=25+
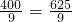 .
.又
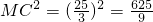 ,
,∴MD2+CD2=MC2.

∴△CDM是直角三角形,且
∠MDC=90°,CD经过半径MD的外端点D,
∴直线CD是⊙M的切线.
(3)解:由已知,AE⊥CD,由(2),MD⊥CD,
∴MD∥AE,
∴△CDM∽△CEA.
∴
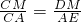 ,即
,即 ,解得AE=8.
,解得AE=8.连接BF.则∠AFB=90°.
又∠MDC=90°,∠CMD=∠CAE,
∴Rt△CDM∽Rt△BFA.
∴
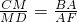 ,即
,即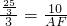 ,解得AF=6.
,解得AF=6.故所求的一个一元二次方程是x2-14x+48=0.
分析:(1)已知A、B的坐标就可以求出直径AB的长,弦心距MB的长,根据垂径定理就可以求出BD的长,即得到D的坐标.根据待定系数法就可以求出CD的解析式.
(2)连接MD,根据M,C,D的坐标就可以得△CDM的三边的长,根据勾股定理的逆定理证明三角形是直角三角形.
(3)易证△CDM∽△CEA,根据相似三角形的对应边的比相等,可以求出AE,再证明Rt△CDM∽Rt△BFA,就可以得到AF,则所求的一元二次方程就可以得到.
点评:本题主要考查了待定系数法求函数解析式,以及相似三角形的性质,相似三角形的对应边的比相等.

练习册系列答案
相关题目
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
