题目内容
操作探究:
我们知道一个三角形中有三条高线和三条中线.如图1,AD和AE分别是△ABC中BC边上的高线和中线,我们规定:kA=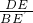 ,另外,对kB、kC作类似的规定.
,另外,对kB、kC作类似的规定.
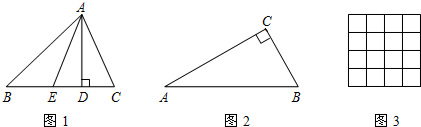
(1)如图2,在△ABC中,∠C=90°,∠A=30°,则kA的值为______,kC的值为______;
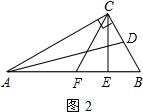
(2)在每个小正方形边长均为1的4×4的方格纸上(如图3),画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且kA=2,面积也为2;
(3)判断下面三个命题的真假(真命题打“√”,假命题的打“×”)
①若△ABC中,kA<1,则△ABC为锐角三角形______;
②若△ABC中,kA=1,则△ABC为直角三角形______;
③若△ABC中,kA>1,则△ABC为钝角三角形______.
 解:(1)在△ABC中,∠C=90°,∠A=30°时,BC边上的高,垂足就是点C,设中线是AD,则kA=
解:(1)在△ABC中,∠C=90°,∠A=30°时,BC边上的高,垂足就是点C,设中线是AD,则kA= =1;
=1;CE⊥AB于E,CF是中线,则CF=
 AB=BF,
AB=BF,又∵∠B=90°-30°=60°,
∴△BCF是等边三角形;
∴EF=BE=
 BF=
BF= AF,
AF,∴kC=
 =
= ;
;(2)作图如下:
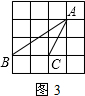 ;
;(3)①(1)中kC=
 ,而△ABC是直角三角形,故命题错误;
,而△ABC是直角三角形,故命题错误;②kA=1时,过顶点A的高线的垂足与三角形的顶点一定重合,故三角新一定是直角三角形,故命题正确;
③kA>1时,过顶点A的高线的垂足与三角形的顶点一定在边的延长线上,则三角形一定是钝角三角形,故命题正确.
故答案是:×,√,√.
分析:(1)根据kA的定义即可直接求解;CE⊥AB于E,CF是中线,可以证明△BCF是等边三角形,根据三线合一定理,以及直角三角形斜边上的中线等于斜边的一半,即可求解;
(2)kA=2,则一定是钝角三角形,作出一边长是2,这边上的高也是2的三角形;
(3)根据(1)即可确定①是错误的;
②③根据kA的值可以确定过顶点A的高线的垂足与三角形的顶点的位置,即可确定三角形的形状.
点评:本题考查了三角形的作图,正确理解kA的意义,根据kA的值可以确定过顶点A的高线的垂足与三角形的顶点的位置是关键.

练习册系列答案
相关题目
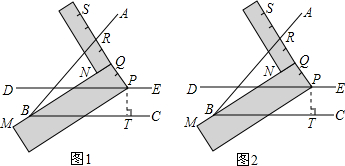 (1)阅读理解:
(1)阅读理解: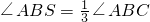 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出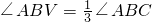 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).