题目内容
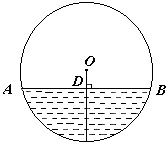
 在直径是52cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度CD为16cm,求油面宽度AB的长.
在直径是52cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度CD为16cm,求油面宽度AB的长.分析:因为圆柱形油槽装入油后形成弓形,可以考虑用垂径定理解答.
解答: 解:由题意得出:OC⊥AB于点D,
解:由题意得出:OC⊥AB于点D,
由垂径定理知,点D为AB的中点,AB=2AD,
∵直径是52cm,
∴OB=26cm,
∴OD=OC-CD=26-16=10(cm),
由勾股定理知,
BD=
=24(cm),
∴AB=48cm.
 解:由题意得出:OC⊥AB于点D,
解:由题意得出:OC⊥AB于点D,由垂径定理知,点D为AB的中点,AB=2AD,
∵直径是52cm,
∴OB=26cm,
∴OD=OC-CD=26-16=10(cm),
由勾股定理知,
BD=
| BO2-OD2 |
∴AB=48cm.
点评:此题考查了勾股定理的应用和垂径定理的应用,圆中的有关半径,弦长,弦心距之间的计算一般是通过垂径定理转化为解直角三角形的问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
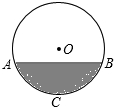 在直径为52cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为16cm,那么油面宽度AB是
在直径为52cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为16cm,那么油面宽度AB是