题目内容
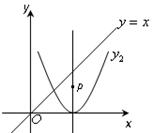
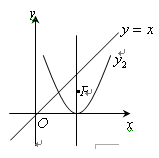
将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象. P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .

【答案】
1或3或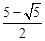 或
或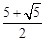 .
.
【解析】
试题分析:∵抛物线y1=2x2向右平移2个单位,∴抛物线y2的函数解析式为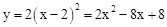 .
.
∴抛物线y2的对称轴为直线x=2.
∵直线x=t与直线y=x、抛物线y2交于点A、B,
∴点A的坐标为(t,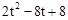 ),点B的坐标为(t,t).∴
),点B的坐标为(t,t).∴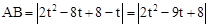 .
.
若△APB是以点A为直角顶点的等腰直角三角形,则P(2,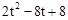 ),
),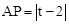 ,∴
,∴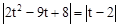 ;
;
若△APB是以点B为直角顶点的等腰直角三角形,则P(2,t),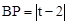 ,∴
,∴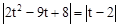 .
.
∴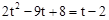 ①或
①或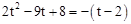 ②.
②.
整理①得,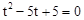 ,解得
,解得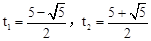 ;
;
整理②得,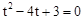 ,解得t1=1,t2=3,
,解得t1=1,t2=3,
综上所述,满足条件的t值为:1或3或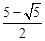 或
或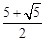 .
.
考点:1.多形式变化问题;2. 二次函数的性质与平移变换;3. 等腰直角三角形的性质;4.解一元二次方程;5.分类思想的应用.

练习册系列答案
相关题目
(1)将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2= ;
(2)如图,P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于
|