题目内容
 判断题:
判断题:甲、乙两人计算算式x+
| 1-2x+x2 |
| 1-2x+x2 |
| (1-x)2 |
| 1-2x+x2 |
| (1-x)2 |
哪一个答案是正确的?为什么?对的说出理由,错的指出错误的原因.
分析:当x>1时,x+
=x+
=x+x-1=2x-1;当x<1时,原式=x+1-x=1由于3>1,所以应该代入前者求值,所以乙的答案是正确的,甲错误.
| 1-2x+x2 |
| (1-x)2 |
解答:解:乙的结果对,
∵x=3,
∴1-x<0且
≥0,
即
=x-1,而不是
=1-x,
∴乙的答案是正确的,甲的答案是错误的.
∵x=3,
∴1-x<0且
| (1-x)2 |
即
| (1-x)2 |
| (1-x)2 |
∴乙的答案是正确的,甲的答案是错误的.
点评:本题主要考查了实数的综合运算能力,对于根号下面含有未知数的,开根号时应注意对未知数的值分类讨论,不同的x值在不同的情况下开根号所得的代数式不相同.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
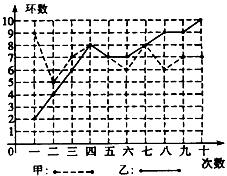 (创新探究题)甲,乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示,请从下列四个不同的角度对这次测试结果进行分析:
(创新探究题)甲,乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示,请从下列四个不同的角度对这次测试结果进行分析: 判断题:
判断题: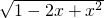 的值,当x=3的时候,得到不同的答案,其中甲的解答是x+
的值,当x=3的时候,得到不同的答案,其中甲的解答是x+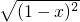 =x+1-x=1;乙的解答是x+
=x+1-x=1;乙的解答是x+