题目内容
 (2010•潍坊)如图所示,抛物线与x轴交于点A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3).以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E,连接DM并延长交⊙M于点N,连接AN、AD.
(2010•潍坊)如图所示,抛物线与x轴交于点A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3).以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E,连接DM并延长交⊙M于点N,连接AN、AD.(1)求抛物线所对应的函数关系式及抛物线的顶点坐标;
(2)若四边形EAMD的面积为
 ,求直线PD的函数关系式;
,求直线PD的函数关系式;(3)抛物线上是否存在点P,使得四边形EAMD的面积等于△DAN的面积?若存在,求出点P的坐标;若不存在,说明理由.
【答案】分析:(1)根据A、B、C的坐标即可用待定系数法求出抛物线的解析式,进而可用配方法求出其顶点坐标;
(2)连接EM,过D作DF⊥x轴于F;由于ED、EA都是⊙O的切线,根据切线长定理可得EA=ED,易证得△EAM≌△EDM则它们的面积相等,由此可得到S△EAM=2 ,即可求出EA的长,也就得到了E点的坐标;在Rt△EAM中,根据EA、AM的值,即可求出∠EMA的度数,进而可求出∠DMF的度数,从而在Rt△DMF中,通过解直角三角形求出MF、DF的长,由此求得D点坐标,用待定系数法即可求出直线DP的解析式;(需注意的是AE的长为正值,但是E点的纵坐标有正负两种情况,所以要分类讨论)
,即可求出EA的长,也就得到了E点的坐标;在Rt△EAM中,根据EA、AM的值,即可求出∠EMA的度数,进而可求出∠DMF的度数,从而在Rt△DMF中,通过解直角三角形求出MF、DF的长,由此求得D点坐标,用待定系数法即可求出直线DP的解析式;(需注意的是AE的长为正值,但是E点的纵坐标有正负两种情况,所以要分类讨论)
(3)在△DAN中,由于DN是⊙M的直径,所以DM=MN,则△DAM和△MAN等底同高,所以面积相等,即△DAN的面积是△DAM的2倍;在(2)题中已经求出四边形EAMD的面积是△EAM的2倍,若四边形EAMD的面积等于△DAN的面积,则△DAM、△EAM的面积相等,这两个三角形共用底边AM,所以它们的高相同,由此可证得PD与x轴平行,即PD的解析式为y=±2,联立抛物线的解析式即可求出P点的坐标.
解答:解:(1)因为抛物线与x轴交于点A(-1,0)、B(3,0)两点,
设抛物线的函数关系式为:y=a(x+1)(x-3),
∵抛物线与y轴交于点C(0,-3),
∴-3=a(0+1)(0-3),
∴a=1,
所以,抛物线的函数关系式为:y=x2-2x-3,(2分)
又∵y=(x-1)2-4,
因此,抛物线的顶点坐标为(1,-4);(3分)
(2)连接EM,∵EA、ED是⊙M的两条切线,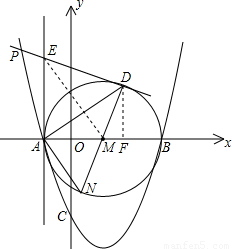
∴EA=ED,EA⊥AM,ED⊥MD,
∴△EAM≌△EDM(HL),
又∵四边形EAMD的面积为 ,
,
∴S△EAM=2 ,
,
∴ AM•AE=2
AM•AE=2 ,
,
又∵AM=2,
∴AE=2 ,
,
因此,点E的坐标为E1(-1,2 )或E2(-1,-2
)或E2(-1,-2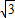 ),(5分)
),(5分)
当E点在第二象限时,切点D在第一象限,
在直角三角形EAM中,tan∠EMA= =
= =
= ,
,
∴∠EMA=60°,
∴∠DMB=60°,
过切点D作DF⊥AB,垂足为点F,
∴MF=1,DF= ,
,
因此,切点D的坐标为(2,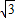 ),(6分)
),(6分)
设直线PD的函数关系式为y=kx+b,
将E(-1,2 ),D(2,
),D(2, )的坐标代入得
)的坐标代入得 ,
,
解之,得: ,
,
所以,直线PD的函数关系式为 ,(7分)
,(7分)
当E点在第三象限时,切点D在第四象限,
同理可求:切点D坐标为(2,- ),
),
直线PD的函数关系式为 ,
,
因此,直线PD的函数关系式为 或
或 ;(8分)
;(8分)
(3)若四边形EAMD的面积等于△DAN的面积,
又∵S四边形EAMD=2S△EAM,S△DAN=2S△AMD,
∴S△AMD=S△EAM,
∴E、D两点到x轴的距离相等,
∵PD与⊙M相切,
∴点D与点E在x轴同侧,
∴切线PD与x轴平行,
此时切线PD的函数关系式为y=2或y=-2,(9分)
当y=2时,由y=x2-2x-3得,x=1± ;
;
当y=-2时,由y=x2-2x-3得,x=1± ,(11分)
,(11分)
故满足条件的点P的位置有4个,分别是P1(1+ ,2)、P2(1-
,2)、P2(1- ,2)、P3(1+
,2)、P3(1+ ,-2)、P4(1-
,-2)、P4(1- ,-2).(12分)
,-2).(12分)
说明:本参考答案给出了一种解题方法,其它正确方法应参考本标准给出相应分数.
点评:此题主要考查了二次函数解析式的确定、切线的性质、切线长定理、全等三角形的判定和性质、图形面积的求法等重要知识,同时还考查了分类讨论的数学思想,综合性强,难度较大.
(2)连接EM,过D作DF⊥x轴于F;由于ED、EA都是⊙O的切线,根据切线长定理可得EA=ED,易证得△EAM≌△EDM则它们的面积相等,由此可得到S△EAM=2
 ,即可求出EA的长,也就得到了E点的坐标;在Rt△EAM中,根据EA、AM的值,即可求出∠EMA的度数,进而可求出∠DMF的度数,从而在Rt△DMF中,通过解直角三角形求出MF、DF的长,由此求得D点坐标,用待定系数法即可求出直线DP的解析式;(需注意的是AE的长为正值,但是E点的纵坐标有正负两种情况,所以要分类讨论)
,即可求出EA的长,也就得到了E点的坐标;在Rt△EAM中,根据EA、AM的值,即可求出∠EMA的度数,进而可求出∠DMF的度数,从而在Rt△DMF中,通过解直角三角形求出MF、DF的长,由此求得D点坐标,用待定系数法即可求出直线DP的解析式;(需注意的是AE的长为正值,但是E点的纵坐标有正负两种情况,所以要分类讨论)(3)在△DAN中,由于DN是⊙M的直径,所以DM=MN,则△DAM和△MAN等底同高,所以面积相等,即△DAN的面积是△DAM的2倍;在(2)题中已经求出四边形EAMD的面积是△EAM的2倍,若四边形EAMD的面积等于△DAN的面积,则△DAM、△EAM的面积相等,这两个三角形共用底边AM,所以它们的高相同,由此可证得PD与x轴平行,即PD的解析式为y=±2,联立抛物线的解析式即可求出P点的坐标.
解答:解:(1)因为抛物线与x轴交于点A(-1,0)、B(3,0)两点,
设抛物线的函数关系式为:y=a(x+1)(x-3),
∵抛物线与y轴交于点C(0,-3),
∴-3=a(0+1)(0-3),
∴a=1,
所以,抛物线的函数关系式为:y=x2-2x-3,(2分)
又∵y=(x-1)2-4,
因此,抛物线的顶点坐标为(1,-4);(3分)
(2)连接EM,∵EA、ED是⊙M的两条切线,

∴EA=ED,EA⊥AM,ED⊥MD,
∴△EAM≌△EDM(HL),
又∵四边形EAMD的面积为
 ,
,∴S△EAM=2
 ,
,∴
 AM•AE=2
AM•AE=2 ,
,又∵AM=2,
∴AE=2
 ,
,因此,点E的坐标为E1(-1,2
 )或E2(-1,-2
)或E2(-1,-2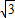 ),(5分)
),(5分)当E点在第二象限时,切点D在第一象限,
在直角三角形EAM中,tan∠EMA=
 =
= =
= ,
,∴∠EMA=60°,
∴∠DMB=60°,
过切点D作DF⊥AB,垂足为点F,
∴MF=1,DF=
 ,
,因此,切点D的坐标为(2,
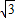 ),(6分)
),(6分)设直线PD的函数关系式为y=kx+b,
将E(-1,2
 ),D(2,
),D(2, )的坐标代入得
)的坐标代入得 ,
,解之,得:
 ,
,所以,直线PD的函数关系式为
 ,(7分)
,(7分)当E点在第三象限时,切点D在第四象限,
同理可求:切点D坐标为(2,-
 ),
),直线PD的函数关系式为
 ,
,因此,直线PD的函数关系式为
 或
或 ;(8分)
;(8分)(3)若四边形EAMD的面积等于△DAN的面积,
又∵S四边形EAMD=2S△EAM,S△DAN=2S△AMD,
∴S△AMD=S△EAM,
∴E、D两点到x轴的距离相等,
∵PD与⊙M相切,
∴点D与点E在x轴同侧,
∴切线PD与x轴平行,
此时切线PD的函数关系式为y=2或y=-2,(9分)
当y=2时,由y=x2-2x-3得,x=1±
 ;
;当y=-2时,由y=x2-2x-3得,x=1±
 ,(11分)
,(11分)故满足条件的点P的位置有4个,分别是P1(1+
 ,2)、P2(1-
,2)、P2(1- ,2)、P3(1+
,2)、P3(1+ ,-2)、P4(1-
,-2)、P4(1- ,-2).(12分)
,-2).(12分)说明:本参考答案给出了一种解题方法,其它正确方法应参考本标准给出相应分数.
点评:此题主要考查了二次函数解析式的确定、切线的性质、切线长定理、全等三角形的判定和性质、图形面积的求法等重要知识,同时还考查了分类讨论的数学思想,综合性强,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010•潍坊)如图所示,抛物线与x轴交于点A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3).以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E,连接DM并延长交⊙M于点N,连接AN、AD.
(2010•潍坊)如图所示,抛物线与x轴交于点A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3).以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E,连接DM并延长交⊙M于点N,连接AN、AD.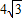 ,求直线PD的函数关系式;
,求直线PD的函数关系式;